НИКОМЕДА КОНХОИДА — плоская алгебраич. кривая 4 го порядка, уравнение к рой в декартовых прямоугольных координатах имеет вид в полярных координатах: Внешняя ветвь (см. рис.). Асимптота x=а. Две точки перегиба Ви С. Внутренняя ветвь. Асимптота х=а. Начало координат… … Математическая энциклопедия
Никомеда конхоида — плоская кривая, впервые рассмотренная древнегреческим геометром Никомедом; см. Линия … Большая советская энциклопедия
Конхоида Никомеда — Три конхоиды прямой с общим центром, красная , зелёная и синяя Конхоида Никомеда ― … Википедия
Конхоида — Две ветви конхоиды окружности с общим центром Конхоида кривой плоская кривая, получающаяся при увеличении или уменьшении радиус вектора каждой точки данной плоской кривой на постоянную величину. Для вычерчивания конхоиды служит прибор… … Википедия
КОНХОИДА Никомеда — (от греч. konchoeides похожий на раковину) алгебраическая кривая 4 го порядка; множество точек М и М , получающееся при увеличении или уменьшении каждого радиус вектора точек данной прямой х = а на одну и ту же величину d. Рассмотрена… … Большой Энциклопедический словарь
КОНХОИДА — Никомеда (от греч. похожий на раковину), алгебр. кривая 4 го порядка (рис.); множество точек М и М , получающееся при увеличении или уменьшении каждого радиус вектора точек данной прямой х = а на одну и ту же величину d. Рассмотрена др. греч.… … Естествознание. Энциклопедический словарь
конхоида — Никомеда (от греч. konchoeidēs похожий на раковину), алгебраическая кривая 4 го порядка; множество точек М и М´, получающееся при увеличении или уменьшении каждого радиус вектора точек данной прямой х = а на одну и ту же величину d. Рассмотрена… … Энциклопедический словарь
КОНХОИДА — кривой плоская кривая, получающаяся при увеличении или уменьшении радиус вектора каждой точки данной плоской кривой на постоянный отрезок l. Если уравнение данной кривой в полярных координатах: р=f(j), то уравнение ее К. имеет вид: Примеры: К.… … Математическая энциклопедия
Математика — Слово математика происходит от греческого μάθημα (наука, учение), в свою очередь происходящего, вместе с имеющим одно с ним значение словом μάθησις, от глагола μανθάνω, первоначальное значение которого, учусь через размышление , устанавливало… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Линия — I Линия (от лат. linea) геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. 1) В элементарной… … Большая советская энциклопедия
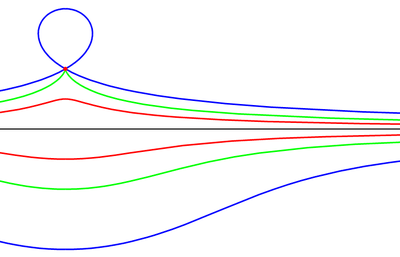 Три конхоиды прямой с общим центром, красная
Три конхоиды прямой с общим центром, красная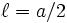 , зелёная
, зелёная  и синяя
и синяя 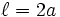
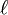 :
: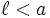 ― изолированная точка
― изолированная точка ― узловая точка
― узловая точка ― точка возврата
― точка возврата .
.
