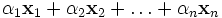- Линейная зависимость
-
Лине́йное простра́нство, или ве́кторное простра́нство — основной объект изучения линейной алгебры.
Содержание
Определение
Линейное, или векторное пространство
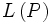 над полем P — это непустое множество L, на котором введены операции
над полем P — это непустое множество L, на котором введены операции- сложения, то есть каждой паре элементов множества
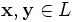 ставится в соответствие элемент того же множества, обозначаемый
ставится в соответствие элемент того же множества, обозначаемый 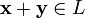 и
и - умножения на скаляр (то есть элемент поля P), то есть любому элементу
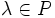 и любому элементу
и любому элементу 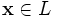 ставится в соответствии элемент из
ставится в соответствии элемент из 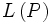 , обозначаемый
, обозначаемый 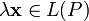 .
.
При этом удовлетворяются следующие условия:
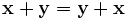 , для любых
, для любых 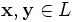 (коммутативность сложения);
(коммутативность сложения);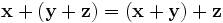 , для любых
, для любых 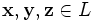 (ассоциативность сложения);
(ассоциативность сложения);- существует такой элемент
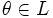 , что
, что 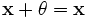 для любого
для любого 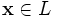 (существование нейтрального элемента относительно сложения), в частности L не пусто;
(существование нейтрального элемента относительно сложения), в частности L не пусто; - для любого
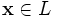 существует такой элемент
существует такой элемент 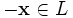 , что
, что 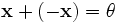 (существование противоположного элемента).
(существование противоположного элемента). 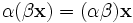 (ассоциативность умножения на скаляр);
(ассоциативность умножения на скаляр);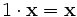 (существование нейтрального элемента относительно умножения).
(существование нейтрального элемента относительно умножения).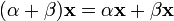 (дистрибутивность умножения на скаляр относительно сложения);
(дистрибутивность умножения на скаляр относительно сложения);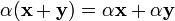 (дистрибутивность сложения относительно умножения на скаляр).
(дистрибутивность сложения относительно умножения на скаляр).
Элементы множества L называют векторами, а элементы поля P — скалярами.
Простейшие свойства
- Нейтральный элемент
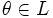 является единственным.
является единственным. 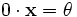 для любого
для любого 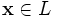 .
.- Для любого
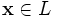 противоположный элемент
противоположный элемент 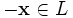 является единственным.
является единственным. 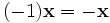 для любого
для любого 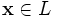 .
.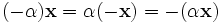 для любых
для любых 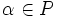 и
и 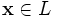 .
.
Связанные определения и свойства
- Линейное подпространство или векторное подпространство ― непустое подмножество P линейного пространства L такое, что P само является линейным пространством по отношению к определенным в L действиям сложения и умножения на скаляр.
- Конечная сумма вида
-
- называется линейной комбинацией элементов
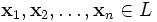 с коэффициентами
с коэффициентами 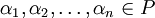 .
.
- Линейная комбинация называется нетривиальной, если хотя бы один из её коэффициентов отличен от нуля.
- Элементы
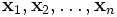 называются линейно зависимыми, если существует нетривиальная линейная комбинация (1), равная элементу
называются линейно зависимыми, если существует нетривиальная линейная комбинация (1), равная элементу 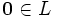 . В противном случае эти элементы называются линейно независимыми.
. В противном случае эти элементы называются линейно независимыми. - Бесконечное подмножество векторов из L называется линейно зависимым, если линейно зависимо его некоторое конечное подмножество, и линейно независимым, если любое его конечное подмножество линейно независимо.
- Число элементов (мощность) максимального линейно независимого подмножества пространства не зависит от выбора этого подмножества и называется рангом, или размерностью, пространства, а само это подмножество — базисом.
- Любые n линейно независимых элементов n-мерного пространства образуют базис этого пространства.
- Любой вектор
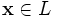 можно представить (единственным образом) в виде конечной линейной комбинации базисных элементов:
можно представить (единственным образом) в виде конечной линейной комбинации базисных элементов:
-
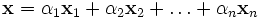 .
.
Примеры
- Нулевое пространство, единственным элементом которого является ноль.
- Пространство всех функций
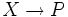 образует векторное пространство размерности равной мощности X.
образует векторное пространство размерности равной мощности X. - поле вещественных чисел может быть рассмотрено как континуально-мерное векторное пространство над полем рациональных чисел.
Дополнительные структуры
- Нормированное векторное пространство
- Топологическое линейное пространство
- Евклидово пространство
- Гильбертово пространство
См. также
- Линейный оператор
- Сопряжённое пространство
- Модуль над кольцом
- Выпуклый функционал
- Линейная независимость
- Линейная оболочка
Литература
- Гельфанд И.М. Лекции по линейной алгебре. изд. МЦНМО, 1998.
Ссылки
- сложения, то есть каждой паре элементов множества
Wikimedia Foundation. 2010.