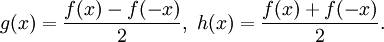Нечетные и четные функции
- Нечетные и четные функции
-
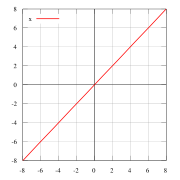
f(x) = x — пример нечётной функции.

f(x) = x2 — пример чётной функции.
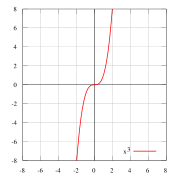
f(x) = x3, нечётная
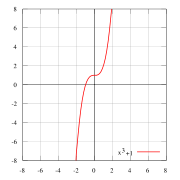
f(x) = x3 + 1 ни чётная, ни нечётная
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.
Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.
Или по-другому
Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.
Определения
- Функция
![f:[-X,X] \subset \mathbb{R} \to \mathbb{R}](/pictures/wiki/files/101/ed5743482e96ed8c5bee8117ee026844.png) называется нечётной, если справедливо равенство
называется нечётной, если справедливо равенство
![f(-x)=-f(x), \quad \forall x \in [-X,X].](/pictures/wiki/files/102/f6ab611fbaf32ad9e732deb96e3fb9ca.png)
- Функция f называется чётной, если справедливо равенство
![f(-x) = f(x),\quad \forall x \in [-X,X].](/pictures/wiki/files/55/712740b91f011d49b277240b725bef17.png)
- Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.
Свойства
- График нечётной функции симметричен относительно начала координат O.
- График чётной функции симметричен относительно оси ординат Oy.
- Произвольная функция
![f:[-X,X] \subset \mathbb{R} \to \mathbb{R}](/pictures/wiki/files/101/ed5743482e96ed8c5bee8117ee026844.png) может быть представлена в виде суммы нечётной и чётной функций:
может быть представлена в виде суммы нечётной и чётной функций:
- f(x) = g(x) + h(x),
где
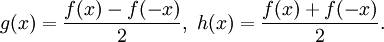
- Функция
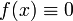 — единственная функция, одновременно являющаяся нечётной и чётной.
— единственная функция, одновременно являющаяся нечётной и чётной.
- Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
- Произведение или дробь двух нечётных функций чётно.
- Произведение или дробь двух чётных функций чётно.
- Произведение или дробь нечётной и чётной функций нечётно.
- Композиция двух нечётных функция нечётна.
- Композиция двух чётных функций чётна.
- Композиция чётной функции с нечётной чётна.
- Композиция любой функции с чётной чётна (но не наоборот).
- Функция, обратная чётной, чётна, а нечётной — нечётна.
- Производная чётной функции нечётна, а нечётной — чётна.
- То же верно про производную третьего, пятого и вообще любого нечётного порядка.
- Производная чётного порядка сохраняет чётность.
Примеры
Нечётные функции
Чётные функции
Вариации и обобщения
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Нечетные и четные функции" в других словарях:
Четные и нечетные функции — f(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
Ряд Фурье — Добавление членов ряда Фурье … Википедия
Ряды Фурье — Ряд Фурье представление произвольной функции f с периодом τ в виде ряда Этот ряд может быть также переписан в виде . где Ak амплитуда k го гармонического колебания (функции cos), кру … Википедия
Фурье ряд — Ряд Фурье представление произвольной функции f с периодом τ в виде ряда Этот ряд может быть также переписан в виде . где Ak амплитуда k го гармонического колебания (функции cos), кру … Википедия
ЛАНДАУ ТЕОРЕМЫ — теоремы для регулярных в круге функций, устанавливающие нек рые связи между геометрич. свойствами производимого этими функциями конформного отображения и начальными коэффициентами представляющих их степенных рядов. В 1904 Э. Ландау показал [1],… … Математическая энциклопедия
МОДУЛЯРНАЯ ФУНКЦИЯ — эллиптическая модулярная функция, одного комплексного переменного автоморфная функция комплексного переменного ассоциированная с группой Г всех дробно линейных преобразований вида где целые действительные числа (эта группа наз. модулярной).… … Математическая энциклопедия
ГОСТ Р ИСО/МЭК 19762-1-2011: Информационные технологии. Технологии автоматической идентификации и сбора данных (АИСД). Гармонизированный словарь. Часть 1. Общие термины в области АИСД — Терминология ГОСТ Р ИСО/МЭК 19762 1 2011: Информационные технологии. Технологии автоматической идентификации и сбора данных (АИСД). Гармонизированный словарь. Часть 1. Общие термины в области АИСД оригинал документа: Accredited Standards… … Словарь-справочник терминов нормативно-технической документации
Суперкомпиляция — Суперкомпиляция специальная техника оптимизации алгоритмов, основанная на знании конкретных входных данных алгоритма. Суперкомпилятор принимает исходный код алгоритма плюс некоторые данные о входных параметрах и возвращает новый исходный… … Википедия
Земляков — Земляков, Александр Николаевич Файл:Zemlyakov.jpg Александр Николаевич Земляков (17 апреля 1950(19500417), Бологое 1 января 2005, Черноголовка) математик,выдающийся советский и российский педагог, автор учебно педагогической… … Википедия
руническое письмо — письменность, употреблявшаяся германцами со II III вв. По мере христианизации Р.ое П.о повсеместно вытесняется латинским алфавитом. Однако в Скандинавии, где Р.ы имели наиболее длительную историю, они были в ходу на протяжении всего… … Словарь средневековой культуры
 f(x) = x — пример нечётной функции.
f(x) = x — пример нечётной функции. f(x) = x2 — пример чётной функции.
f(x) = x2 — пример чётной функции. f(x) = x3, нечётная
f(x) = x3, нечётная f(x) = x3 + 1 ни чётная, ни нечётная
f(x) = x3 + 1 ни чётная, ни нечётная![f:[-X,X] \subset \mathbb{R} \to \mathbb{R}](/pictures/wiki/files/101/ed5743482e96ed8c5bee8117ee026844.png) называется нечётной, если справедливо равенство
называется нечётной, если справедливо равенство![f:[-X,X] \subset \mathbb{R} \to \mathbb{R}](/pictures/wiki/files/101/ed5743482e96ed8c5bee8117ee026844.png) может быть представлена в виде суммы нечётной и чётной функций:
может быть представлена в виде суммы нечётной и чётной функций: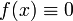 — единственная функция, одновременно являющаяся нечётной и чётной.
— единственная функция, одновременно являющаяся нечётной и чётной.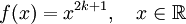 где
где 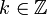 — произвольное целое число.
— произвольное целое число.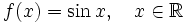 .
.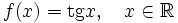 .
.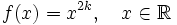 где
где 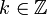 — произвольное целое число.
— произвольное целое число.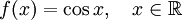 .
.
![f(-x)=-f(x), \quad \forall x \in [-X,X].](/pictures/wiki/files/102/f6ab611fbaf32ad9e732deb96e3fb9ca.png)
![f(-x) = f(x),\quad \forall x \in [-X,X].](/pictures/wiki/files/55/712740b91f011d49b277240b725bef17.png)