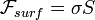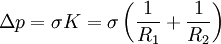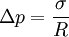Межфазное натяжение

Монета, лежащая на воде в силу поверхностного натяжения

Механика сплошных сред

Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоэластичность Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнения Навье — Стокса · Уравнение диффузии · Закон Гука Известные учёные Ньютон · Гук Бернулли · Эйлер · Коши · Стокс · Навье

Пове́рхностное натяже́ние — термодинамическая характеристика поверхности раздела двух находящихся в равновесии фаз, определяемая работой обратимого изотермокинетического образования единицы площади этой поверхности раздела при условии, что температура, объем системы и химические потенциалы всех компонентов в обеих фазах остаются постоянными.

Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует. Сила поверхностного натяжения пропорциональна длине того участка контура, на который она действует. Коэффициент пропорциональности γ — сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения. Он измеряется в ньютонах на метр. Но более правильно дать определение поверхностному натяжению, как энергии (Дж) на разрыв единицы поверхности (м²). В этом случае появляется физический смысл и связь понятия поверхностного натяжения с внутренней энергией, что было доказано теоретически (Журнал физической химии. 1983, № 10)

Поверхностное натяжение может быть на границе газообразных, жидких и твёрдых тел. Обычно имеется в виду поверхностное натяжение жидких тел на границе «жидкость — газ». В случае жидкой поверхности раздела поверхностное натяжение правомерно также рассматривать как силу, действующую на единицу длины контура поверхности и стремящуюся сократить поверхность до минимума при заданных объёмах фаз.

В общем случае прибор для измерения поверхностного натяжения называется тензиометр.

Проявления

Водомерка на поверхности воды.

Так как появление поверхности жидкости требует совершения работы, каждая среда «стремится» уменьшить площадь своей поверхности:

• в невесомости капля принимает сферическую форму (сфера имеет наименьшую площадь поверхности среди всех фигур одинаковой ёмкости).
• струя воды «слипается» в цилиндр.
• маленькие объекты с плотностью, большей плотности жидкости, способны «плавать» на поверхности жидкости, так как сила тяготения меньше силы, препятствующей увеличению площади жидкости.
• некоторые насекомые (например, Водомерки) способны передвигаться по воде, удерживаясь на её поверхности за счёт сил поверхностного натяжения.
• На многих поверхностях, именуемых несмачиваемыми, вода (или другая жидкость) собирается в капли.

Математическая теория

Площадь поверхности

С поверхностью жидкости связана свободная энергия

$\mathcal{F}_{surf} = \sigma S$

где σ — коэффициент поверхностного натяжения, S — полная площадь поверхности жидкости^[1]. Так как свободная энергия изолированной системы стремится к минимуму, то жидкость (в отсутствие внешних полей) стремится принять форму, имеющую минимальную площадь поверхности. Таких образом задача о форме жидкости сводится к изопериметрической задаче при заданных дополнительных условиях (начальное распределение, объём и т. п.). Свободная капля принимает форму шара, однако при более сложных условиях задача о форме поверхности жидкости становится исключительно сложной.

Формула Лапласа

Рассмотрим тонкую жидкую плёнку, толщиной которой можно пренебречь. Стремясь минимизировать свою свободную энергию, плёнка создаёт разность давления с разных сторон. Этим объясняется существование мыльных пузырей: плёнка сжимается до тех пор, пока давление внутри пузыря не будет превышать атмосферное на величину добавочного давления плёнки. Добавочное давление в точке поверхности зависит от средней кривизны в этой точке и даётся формулой Лапласа:

$\Delta p = \sigma K = \sigma \left({1\over R_1} + {1\over R_2}\right)$

Здесь R_1,2 — радиусы главных кривизн в точке. Они имеют одинаковый знак, если соответствующие центры кривизны лежат по одну сторону от касательной плоскости в точке, и разный знак — если по разную cторону. Например, для сферы центры кривизны в любой точке поверхности совпадают с центром сферы, поэтому

R₁ = R₂ = R

$\Delta p = {2\sigma \over R}$

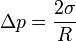
Для случая поверхности кругового цилиндра радиуса R имеем

$R_1 = R, ~~~R_2 = \infty$

$\Delta p = {\sigma \over R}$

Обратите внимание, что Δp должно быть непрерывной функцией на поверхности плёнки, так что выбор «положительной» стороны плёнки в одной точке локально однозначно задаёт положительную сторону поверхности в достаточно близких её точках.

Из формулы Лапласа следует, что свободная мыльная плёнка, натянутая на рамку произвольной формы и не образующая пузырей, будет иметь среднюю кривизну, равную 0.

Способы определения

Способы определения поверхностного натяжения делятся на статические и динамические. В статических методах поверхностное натяжение определяется у сформировавшейся поверхности, находящейся в равновесии. Динамические методы связаны с разрушением поверхностного слоя. В случае измерения поверхностного натяжения растворов (особенно полимеров или ПАВ) следует пользоваться статическими методами. В ряде случаев равновесие на поверхности может наступать в течение нескольких часов (например, в случае концентрированных растворов полимеров с высокой вязкостью). Динамические методы могут быть применены для определения равновесного поверхностного натяжения и динамического поверхностного натяжения. Например, для раствора мыла после перемешивания поверхностное натяжение 58 Дж/м2, а после отстаивания — 35 Дж/м2 . То есть поверхностное натяжение меняется. До установления равновесного оно будет динамическое.

Статические методы:

1. Метод поднятия в капилляре
2. Метод Вильгельми
3. Метод лежачей капли
4. Метод определения по форме висячей капли.
5. Метод вращающейся капли

Динамические методы:

1. Метод Дю Нуи (метод отрыва кольца).
2. Сталагмометрический, или метод счета капель.
3. Метод максимального давления пузырька.
4. Метод осциллирующей струи
5. Метод стоячих волн

Методы

Полностью стандартизованные методы измерений описываются в соответствующих ГОСТ и т. д.

Метод вращающейся капли

Сущностью метода является измерение диаметра капли жидкости, вращающейся в более тяжелой жидкости. Этот способ измерения годится для измерения низких или сверхнизких значений межфазного натяжения. Он широко применяется для микроэмульсий, измерения эффективности ПАВ в нефтедобыче, а также для определения адсорбционных свойств.

Метод Дю Нуи (метод отрыва кольца)

Метод является классическим. Сущность метода вытекает из названия. Платиновое кольцо поднимают из жидкости, смачивающей его, усилие отрыва и есть сила поверхностного натяжения и может быть пересчитано в поверхностную энергию. Метод подходит для измерения ПАВ, трансформаторных масел и т. д.

Поверхностное натяжение жидкостей на границе с воздухом

Вещество	Температура °C	Поверхностное натяжение(10-3 Н/м)
Хлорид натрия 6.0M водный раствор	20	82,55
Хлорид натрия	801	115
Глицерин	30	64,7
Олово	400	518
Азотная кислота 70 %	20	59,4
Анилин	20	42,9
Ацетон	20	23,7
Бензол	20	29,0
Вода	20	72,86
Глицерин	20	59,4
Нефть	20	26
Ртуть	20	486,5
Ртуть	25	485,5
Ртуть	30	484,5
Серная кислота 85 %	20	57,4
Спирт этиловый	20	22,8
Уксусная кислота	20	27,8
Эфир этиловый	20	16,9
Раствор мыла	20	40

Примечания

1. ↑ Обратите внимание, что плёнка, вроде стенки мыльного пузыря, имеет две стороны, так что площадь поверхности жидкости в два раза больше площади плёнки.

См. также

Тензиометр

Внешние ссылки

• методы измерения поверхностного натяжения и их применимость