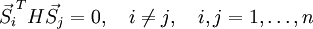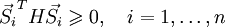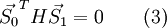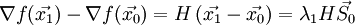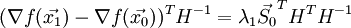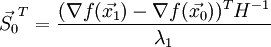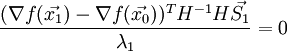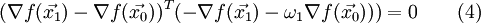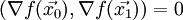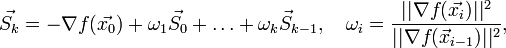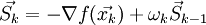- Метод сопряжённых направлений
-
Метод сопряженных градиентов — метод нахождения локального минимума функции на основе информации о её значениях и её градиенте. В случае квадратичной функции в
 минимум находится за n шагов.
минимум находится за n шагов.Содержание
Основные понятия
Определим терминологию:
Пусть
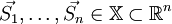 .
.Введём на
 целевую функцию
целевую функцию 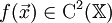 .
.Вектора
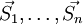 называются сопряжёнными, если:
называются сопряжёнными, если:где
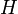 — матрица Гессе
— матрица Гессе 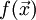 .
.
Теорема (о существовании).
Существует хотя бы одна система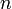 сопряжённых направлений для матрицы
сопряжённых направлений для матрицы 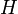 , т.к. сама матрица
, т.к. сама матрица 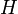 (её собственные вектора) представляет собой такую систему.
(её собственные вектора) представляет собой такую систему.Обоснование метода
Нулевая итерация
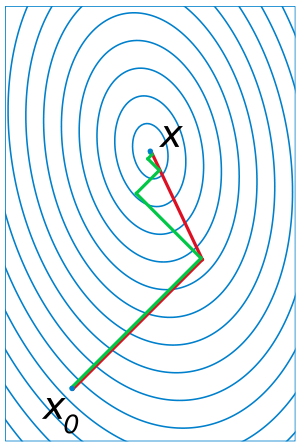 Иллюстрация последовательных приближений метода сопряжённых градиентов к точке экстремума. Картинка наглядно показывает, что каждое последующее сопряжённое направление перпендикулярно предыдущему.
Иллюстрация последовательных приближений метода сопряжённых градиентов к точке экстремума. Картинка наглядно показывает, что каждое последующее сопряжённое направление перпендикулярно предыдущему.Пусть
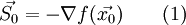
Тогда
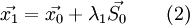 .
.Определим направление
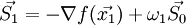 так, чтобы оно было сопряжено с
так, чтобы оно было сопряжено с 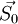 :
:Разложим
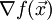 в окрестности
в окрестности 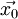 и подставим
и подставим 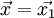 :
:Транспонируем полученное выражение и домножаем на
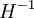 справа:
справа:В силу непрерывности вторых частных производных
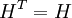 . Тогда:
. Тогда:Подставим полученное выражение в (3):
Тогда, воспользовавшись (1) и (2):
Если
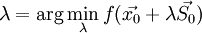 , то градиент в точке
, то градиент в точке 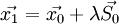 перпендикулярен градиенту в точке
перпендикулярен градиенту в точке 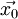 , тогда по правилам скалярного произведения векторов:
, тогда по правилам скалярного произведения векторов:Приняв во внимание последнее, получим из выражения (4) окончательную формулу для вычисления
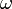 :
:К-я итерация
На k-й итерации имеем набор
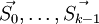 .
.Тогда следующее направление вычисляется по формуле:
где
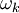 непосредственно рассчитывается на k-й итерации, а все остальные уже были рассчитаны на предыдущих.
непосредственно рассчитывается на k-й итерации, а все остальные уже были рассчитаны на предыдущих.Это выражение может быть переписано в более удобном итеративном виде:
Алгоритм
- Пусть
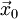 — начальная точка,
— начальная точка, 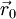 — направление антиградиента и мы пытаемся найти минимум функции
— направление антиградиента и мы пытаемся найти минимум функции 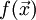 . Положим
. Положим 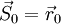 и найдем минимум вдоль направления
и найдем минимум вдоль направления 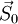 . Обозначим точку минимума
. Обозначим точку минимума 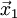 .
.
- Пусть на некотором шаге мы находимся в точке
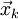 , и
, и 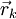 — направление антиградиента. Положим
— направление антиградиента. Положим 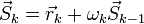 , где
, где 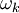 выбирают либо
выбирают либо 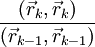 (стандартный алгоритм), либо
(стандартный алгоритм), либо 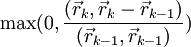 (алгоритм Полака–Райбера). После чего найдем минимум в направлении
(алгоритм Полака–Райбера). После чего найдем минимум в направлении 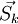 и обозначим точку минимума
и обозначим точку минимума 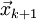 . Если в вычисленном направлении функция не уменьшается, то нужно забыть предыдущее направление, положив
. Если в вычисленном направлении функция не уменьшается, то нужно забыть предыдущее направление, положив 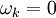 и повторив шаг.
и повторив шаг.
Формализация
- Задаются начальным приближением и погрешностью:
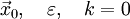
- Рассчитывают начальное направление:
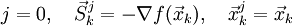
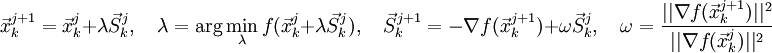
- Если
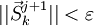 или
или 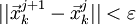 , то
, то 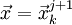 и останов.
и останов. - Иначе
- если
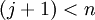 , то
, то 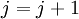 и переход к 3;
и переход к 3; - иначе
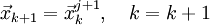 и переход к 2.
и переход к 2.
- если
- Если
Случай квадратичной функции

Теорема.
Если сопряжённые направления используются для поиска минимума квадратичной функции, то эта функция может быть минимизирована за n шагов, по одному в каждом направлении, причём порядок несущественен.Литература
- Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. — М.: Высш. шк., 1986.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
- Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
- Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
- Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
См. также
Ссылки
Wikimedia Foundation. 2010.