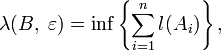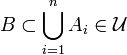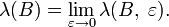Линейная мера

Мера Хаусдорфа — собирательное название класса мер, определённых на борелевской σ-алгебре $\mathcal{B}(X)$ метрического пространства X.

Определение

Ф. Хаусдорф рассматривал^[1] некоторый класс 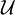$\mathcal{U}$ открытых подмножеств X, на котором определил неотрицательную функцию 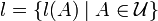$l=\{l(A)\mid A\in\mathcal{U}\}$ и

$\lambda(B,\;\varepsilon)=\inf\left\{\sum_{i=1}^n l(A_i)\right\},$

где нижняя грань берётся по всем конечным или счётным покрытиям борелевского множества 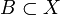$B\subset X$ множествами из 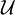$\mathcal{U}$ с диаметром, не превосходящим $\varepsilon$, то есть

$B\subset\bigcup_{i=1}^n A_i\in\mathcal{U}$

и

$\mathrm{diam}\,A_i\leqslant\varepsilon,\quad n=1,\;2,\;\ldots$

Мерой Хаусдорфа λ, определяемой классом 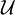$\mathcal{U}$ и функцией l, называется предел

$\lambda(B)=\lim_{\varepsilon\to 0}\lambda(B,\;\varepsilon).$

Примеры

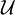1. Пусть $\mathcal{U}$ — совокупность всех шаров в X, a 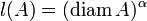$l(A)=(\mathrm{diam}\,A)^\alpha$, где α > 0. Тогда соответствующая мера λ будет называться α-мерой Хаусдорфа. При α = 1 такая мера будет называться линейной мерой Хаусдорфа, а при α = 2 — плоской мерой Хаусдорфа.
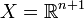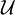2. Если $X=\R^{n+1}$, $\mathcal{U}$ — совокупность цилиндров с шаровыми основаниями и осями, параллельными направлению оси x_{n + 1} и l(A) равна n-мерному объёму осевого сечения цилиндра 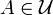$A\in\mathcal{U}$, то соответствующая мера Хаусдорфа называется цилиндрической мерой.

Литература

• Данфорд, Н., Шварц, Дж. Линейные операторы. Общая теория. — пер. с англ.. — М.: Едиториал УРСС, 2004. — Т. 1. — 896 с. — ISBN 5-354-00601-5.

Примечания

1. ↑ Hausdorff, F. Mathematische Annalen. — 1918. — Bd 79. — S. 157—179.