Бета распределение

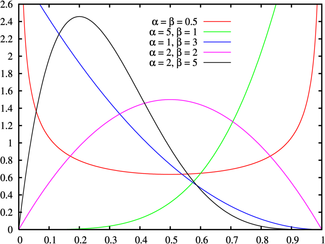
Бета-распределение

Плотность вероятности
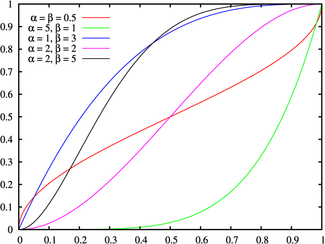
Функция распределения
Параметры	α > 0 β > 0
Носитель	$x \in [0, 1]\!$
Плотность вероятности	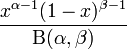$\frac{x^{\alpha-1}(1-x)^{\beta-1}} {\mathrm{B}(\alpha,\beta)}\!$
Функция распределения	$I_x(\alpha,\beta)\!$
Математическое ожидание	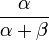$\frac{\alpha}{\alpha+\beta}\!$
Медиана
Мода	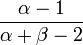$\frac{\alpha-1}{\alpha+\beta-2}\!$ для α > 1,β > 1
Дисперсия	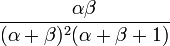$\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\!$
Коэффициент асимметрии	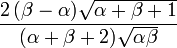$\frac{2\,(\beta-\alpha)\sqrt{\alpha+\beta+1}}{(\alpha+\beta+2)\sqrt{\alpha\beta}}$
Коэффициент эксцесса	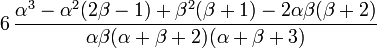$6\,\frac{\alpha^3-\alpha^2(2\beta-1)+\beta^2(\beta+1)-2\alpha\beta(\beta+2)} {\alpha \beta (\alpha+\beta+2) (\alpha+\beta+3)}\!$
Информационная энтропия
Производящая функция моментов	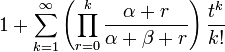$1 +\sum_{k=1}^{\infty} \left( \prod_{r=0}^{k} \frac{\alpha+r}{\alpha+\beta+r} \right) \frac{t^k}{k!}$
Характеристическая функция	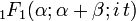${}_1F_1(\alpha; \alpha+\beta; i\,t)\!$

Бе́та распределе́ние в теории вероятностей и статистике — двухпараметрическое семейство абсолютно непрерывных распределений.

Определение

Пусть распределение случайной величины X задаётся плотностью вероятности f_X, имеющей вид:

$f_X(x) = \frac{1}{\mathrm{B}(\alpha, \beta)}\, x^{\alpha - 1} (1-x)^{\beta - 1}$,

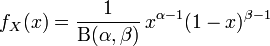где

• α,β > 0 произвольные фиксированные параметры, и
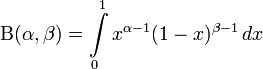• $\mathrm{B}(\alpha,\beta) = \int\limits_0^1 x^{\alpha - 1} (1-x)^{\beta - 1}\, dx$ — бета-функция.

Тогда случайная величина X имеет бета-распределение. Пишут: X˜B(α,β).

Форма графика

Форма графика плотности вероятности бета-распределения зависит от выбора параметров α и β.

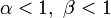• $\alpha < 1,\ \beta < 1$ — график выпуклый и уходит в бесконечность на границах (красная кривая);
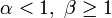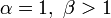• $\alpha < 1,\ \beta \geq 1$ или $\alpha = 1,\ \beta > 1$ — график строго убывающий (синяя кривая)
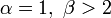  • $\alpha = 1,\ \beta > 2$ — график строго выпуклый;
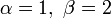  • $\alpha = 1,\ \beta = 2$ — график является прямой линией;
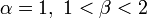  • $\alpha = 1,\ 1 < \beta < 2$ — график строго вогнутый;
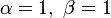• $\alpha = 1,\ \beta = 1$ график совпадает с графиком плотности стандартного непрерывного равномерного распределения;
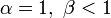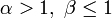• $\alpha = 1,\ \beta < 1$ или $\alpha > 1,\ \beta \leq 1$ — график строго возрастающий (зелёная кривая);
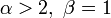  • $\alpha > 2,\ \beta = 1$ — график строго выпуклый;
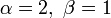  • $\alpha = 2,\ \beta = 1$ — график является прямой линией;
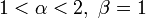  • $1 < \alpha < 2,\ \beta = 1$ — график строго вогнутый;
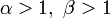• $\alpha > 1,\ \beta > 1$ — график унимодальный (пурпурная и чёрная кривые)

В случае, когда α = β, плотность вероятности симметрична относительно 1 / 2 (красная и пурпурная кривые), то есть

$f_X(x-1/2) = f_X(x+1/2),\; x\in [0,1/2]$.

Моменты

Математическое ожидание и дисперсия случайной величины X, имеющей бета-распределение, имеют вид:

$\mathbb{E}[X] = \frac{\alpha}{\alpha+\beta}$,

$\mathrm{D}[X] = \frac{\alpha \beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$.

Связь с другими распределениями

• Стандартное непрерывное равномерное распределение является частным случаем бета-распределения:

$\mathrm{U}[0,1] \equiv \mathrm{B}(1,1)$.

• Если X,Y — независимые гамма распределённые случайные величины, причём X˜Γ(α,1), а Y˜Γ(β,1), то

$\frac{X}{X+Y} \sim \mathrm{B}(\alpha, \beta)$ .

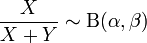Вероятностные распределения Одномерные Многомерные Дискретные: Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | равномерное мультиномиальное Абсолютно непрерывные: Бета | Вейбулла | Гамма | Колмогорова | Коши | Лапласа | логнормальное | Лоренца | нормальное (Гаусса) | равномерное | Парето | Стьюдента | Фишера | хи-квадрат | экспоненциальное | Эрланга многомерное нормальное

править