- Распределение Пуассона
-
Распределение Пуассона Функция вероятности
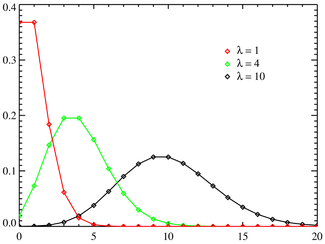
Функция распределения
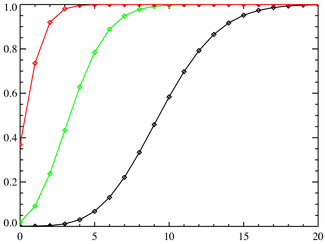
Обозначение 
Параметры 
Носитель 
Функция вероятности 
Функция распределения 
Математическое ожидание 
Медиана 
Мода 
Дисперсия 
Коэффициент асимметрии 
Коэффициент эксцесса 
Информационная энтропия ![\lambda[1\!-\!\ln(\lambda)]\!+\!e^{-\lambda}\sum_{k=0}^\infty \frac{\lambda^k\ln(k!)}{k!}](36f5766e9855c58b14b1b542b27c7812.png)
Производящая функция моментов 
Характеристическая функция 
Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Распределение Пуассона играет ключевую роль в теории массового обслуживания.
Содержание
Определение
Выберем фиксированное число
 и определим дискретное распределение, задаваемое следующей функцией вероятности:
и определим дискретное распределение, задаваемое следующей функцией вероятности: ,
,
где
 обозначает факториал числа
обозначает факториал числа  ,
, — основание натурального логарифма.
— основание натурального логарифма.
Тот факт, что случайная величина
 имеет распределение Пуассона с параметром
имеет распределение Пуассона с параметром  , записывается:
, записывается:  .
.Моменты
Производящая функция моментов распределения Пуассона имеет вид:
 ,
,
откуда
![\mathbb{M}[Y]=\lambda](45a29047c5c2f5af2517b0b1d3ba3031.png) ,
,![\mathbb{D}[Y]=\lambda](5c7ba9764790a76f44a167851cbc036a.png) .
.
Для факториальных моментов распределения справедлива общая формула:
![\mathbb{M}Y^{[k]}=\lambda^k](08bf7faec51c8d0cc743c9e54c0d62fe.png) ,
,
где

А так как моменты и факториальные моменты линейным образом связаны, то часто для пуассоновского распределения исследуются именно факториальные моменты, из которых при необходимости можно вывести и обычные моменты.
Свойства распределения Пуассона
- Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть
 . Тогда
. Тогда
 .
.
- Пусть
 , и
, и  . Тогда условное распределение
. Тогда условное распределение  при условии, что
при условии, что  , биномиально. Более точно:
, биномиально. Более точно:
 .
.
История
Изначально распределение Пуассона было предложено для моделирования потока входящих телефонных звонков на коммутатор. Примеры других ситуаций, которые можно смоделировать, применив это распределение: поломки оборудования, длительность исполнения ремонтных работ стабильно работающим сотрудником, ошибка печати, рост колонии бактерий в чашке Петри, дефекты в длинной ленте или цепи и др.[1].
См. также
Примечания
Литература
- Вентцель Е. С., Овчаров Л. А., Теория вероятностей и её инженерные приложения, М.: 2000, С. 135. — ISBN 978-5-406-00565-1.
- Ральф Винс Математика управления капиталом: Методы анализа риска для трейдеров и портфельных менеджеров = The mathematics of money management risk analysis techniques for traders. — М.: «Альпина Паблишер», 2012. — 400 с. — ISBN 978-5-9614-1894-1
Одномерные Многомерные Дискретные: Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное мультиномиальное Абсолютно непрерывные: Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma многомерное нормальное | копула Для улучшения этой статьи желательно?: - Проверить достоверность указанной в статье информации.
- Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.
Категория:- Дискретные распределения
Wikimedia Foundation. 2010.
