Распределение Коши

Распределение Коши

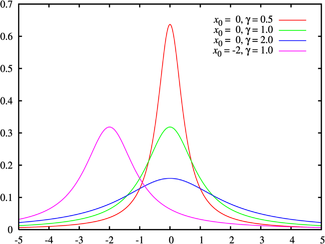
Плотность вероятности Зелёная кривая соответствует стандартному распределению Коши
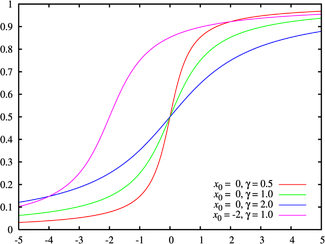
Функция распределения Цвета находятся в соответствии с графиком выше
Обозначение	{{{notation}}}
Параметры	$x_0\!$ — коэффициент сдвига $\gamma > 0\!$ — коэффициент масштаба
Носитель	$x \in (-\infty; +\infty)\!$
Плотность вероятности	$\frac{1}{\pi\gamma\,\left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]} \!$
Функция распределения	$\frac{1}{\pi} \mathrm{arctg}\left(\frac{x-x_0}{\gamma}\right)+\frac{1}{2}$
Математическое ожидание	(не существует)
Медиана	$x_0\!$
Мода	$x_0\!$
Дисперсия	(не существует)
Коэффициент асимметрии	(не существует)
Коэффициент эксцесса	(не существует)
Информационная энтропия	$\ln(4\,\pi\,\gamma)\!$
Производящая функция моментов	(не определена)
Характеристическая функция	$\exp(x_0\,i\,t-\gamma\,|t|)\!$

Распределе́ние Коши́ в теории вероятностей (также называемое в физике распределе́нием Ло́ренца и распределе́нием Бре́йта — Ви́гнера) — класс абсолютно непрерывных распределений. Случайная величина, имеющая распределение Коши, является стандартным примером величины, не имеющей математического ожидания и дисперсии.

Определение

Пусть распределение случайной величины $~X$ задаётся плотностью $~f_X(x)$, имеющей вид:

$f_X(x) = \frac{1}{\pi\gamma \left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]} = { 1 \over \pi } \left[ { \gamma \over (x - x_0)^2 + \gamma^2 } \right]$,

где

• $x_0 \in \mathbb{R}$ — параметр сдвига;
• $\gamma > 0$ — параметр масштаба.

Тогда говорят, что $X$ имеет распределение Коши и пишут $X \sim \mathrm{C}(x_0,\gamma)$. Если $x_0 = 0$ и $\gamma = 1$, то такое распределение называется станда́ртным распределением Коши.

Функция распределения

Функция распределения Коши имеет вид:

$F_X(x) = \frac{1}{\pi}\,\mathrm{arctg}\,\left(\frac{x-x_0}{\gamma}\right)+\frac{1}{2}$.

Она строго возрастает и имеет обратную функцию:

$F^{-1}_X(x) = x_0 + \gamma\,\mathrm{tg}\,\left[\pi\,\left(x-{1 \over 2}\right)\right].$

Это позволяет генерировать выборку из распределения Коши с помощью метода обратного преобразования.

Моменты

Так как интеграл Лебега

$\int\limits_{-\infty}^{\infty}\!x^{\alpha}f_X(x)\, dx$

не определён для $\alpha \geqslant 1$, ни математическое ожидание (хотя интеграл 1-го момента в смысле главного значения равен: $\lim\limits_{c \rightarrow \infty} \int\limits_{-c}^{c} x \cdot { 1 \over \pi } \left[ { \gamma \over (x - x_0)^2 + \gamma^2 } \right]\, dx = x_0$ ), ни дисперсия, ни моменты старших порядков этого распределения не определены. Иногда говорят, что математическое ожидание не определено, а дисперсия бесконечна.

Другие свойства

• Распределение Коши бесконечно делимо.
• Распределение Коши устойчиво. В частности, выборочное среднее выборки из стандартного распределения Коши само имеет стандартное распределение Коши: если $X_1,\ldots, X_n \sim \mathrm{C}(0,1)$, то

$\overline{X} = \frac{1}{n} \sum\limits_{i=1}^n X_i \sim \mathrm{C}(0,1)$

Связь с другими распределениями

• Если $U \sim U[0,1]$, то

$x_0 + \gamma\,\mathrm{tg}\,\left[\pi\left(U-{1 \over 2}\right)\right] \sim \mathrm{C}(x_0,\gamma)$.

• Если $X_1,X_2\!$ — независимые нормальные случайные величины, такие что $X_i \sim \mathrm{N}(0,1),\; i=1,2$, то

$\frac{X_1}{X_2} \sim \mathrm{C}(0,1)$.

• Стандартное распределение Коши является частным случаем распределения Стьюдента:

$\mathrm{C}(0,1) \equiv \mathrm{t}(1)$.

Появление в практических задачах

• Распределением Коши характеризуется длина отрезка, отсекаемого на оси абсцисс прямой, закреплённой в точке на оси ординат, если угол между прямой и осью ординат имеет равномерное распределение на интервале (−π; π) (т.е. направление прямой изотропно на плоскости).
• В физике распределением Коши (называемым также формой Лоренца) описываются профили равномерно уширенных спектральных линий.
• Распределение Коши описывает амплитудно-частотные характеристики линейных колебательных систем в окрестности резонансных частот.

	п·Вероятностные распределения
	Одномерные	Многомерные
Дискретные:	Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное	мультиномиальное
Абсолютно непрерывные:	Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma	многомерное нормальное | копула