Логнормальное распределение

Логнормальное

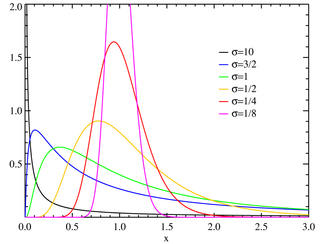
Плотность вероятности μ=0
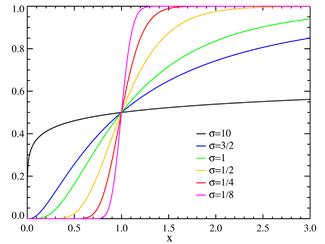
Функция распределения μ=0
Обозначение	$\ln N(\mu,\sigma^2)\,$
Параметры	$\sigma \ge 0$ $-\infty \le \mu \le \infty$
Носитель	$x \in [0; +\infty)\!$
Плотность вероятности	$\exp\left(-\left.\left[\frac{\ln(x)-\mu}{\sigma}\right]^2\right/2\right) \left/ \left(x\sigma\sqrt{2\pi}\right) \right.$
Функция распределения	$\frac{1}{2}+\frac{1}{2} \mathrm{Erf}\left[\frac{\ln(x)-\mu}{\sigma\sqrt{2}}\right]$
Математическое ожидание	$e^{\mu+\sigma^2/2}$
Медиана	$e^{\mu}$
Мода	$e^{\mu-\sigma^2}$
Дисперсия	$(e^{\sigma^2}\!\!-1) e^{2\mu+\sigma^2}$
Коэффициент асимметрии	$e^{-\mu-\sigma^2/2}(e^{\sigma^2}\!\!+2)\sqrt{e^{\sigma^2}\!\!-1}$
Коэффициент эксцесса	$e^{4\sigma^2}\!\!+2e^{3\sigma^2}\!\!+3e^{2\sigma^2}\!\!-6$
Информационная энтропия	$\frac{1}{2}+\frac{1}{2}\ln(2\pi\sigma^2) + \mu$
Производящая функция моментов	$\operatorname{E}[X^s] = e^{s\mu + \tfrac{1}{2}s^2\sigma^2}.$
Характеристическая функция	$\sum_{n=0}^{\infty}\frac{(it)^n}{n!}e^{n\mu+n^2\sigma^2/2}$

Логнорма́льное распределе́ние в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Если случайная величина имеет логнормальное распределение, то её логарифм имеет нормальное распределение.

Определение

Пусть распределение случайной величины $X$ задаётся плотностью вероятности, имеющей вид:

$f_X(x) = \left\{ \begin{matrix} \frac{1}{x \sigma \sqrt{2 \pi}} e^{-(\ln x - \mu)^2/2\sigma^2}, & x > 0 \\ 0, & x \le 0 \end{matrix} \right.$,

где $\sigma>0,\; \mu\in \mathbb{R}$. Тогда говорят, что $X$ имеет логнормальное распределение с параметрами $\mu$ и $\sigma$. Пишут: $X \sim \mathrm{LogN}(\mu,\sigma^2) \$.

Моменты

Формула для $k$-го момента логнормальной случайной величины $X$ имеет вид:

$\mathbb{E}\left[X^k\right] = e^{k\mu + \frac{k^2\sigma^2}{2}},\; k \in \mathbb{N},$

откуда в частности:

$\mathbb{E}[X] = e^{\mu + {\sigma^2 \over 2}}$,

$\mathrm{D}[X] =\left(e^{\sigma^2}-1\right) e^{2\mu + \sigma^2}$.

Любые нецентральные моменты n-мерного совместного логнормального распределения могут быть вычислены по простой формуле:

$\alpha_{n} = e^{ (\mu, n) + \frac{1}{2}(n, \Sigma n)}$, где $\mu$ и $\Sigma$ — параметры многомерного совместного распределения. $n$ — вектор, компоненты которого задают порядок момента. (Например, в двухмерном случае, $n=(2,0)$ — второй нецентральный момент первой компоненты, $n=(1,1)$ — смешанный второй момент). Круглые скобки обозначают скалярное произведение.

Свойства логнормального распределения

• Если $X_1,\ldots, X_n$ — независимые логнормальные случайные величины, такие что $X_i \sim \mathrm{LogN}(\mu, \sigma_i^2)$, то их произведение также логнормально:

$Y = \prod\limits_{i=1}^n X_i \sim \mathrm{LogN}\left(n\mu, \sum\limits_{i=1}^n \sigma^2_i\right)$.

Связь с другими распределениями

• Если $X \sim \mathrm{LogN}(\mu,\sigma^2) \$, то

$Y = \ln X \sim \mathrm{N}(\mu,\sigma^2) \$.

Моделирование логнормальных случайных величин

Для моделирования обычно используется связь с нормальным распределением. Поэтому, достаточно сгенерировать нормально распределённую случайную величину, например, используя преобразование Бокса — Мюллера, и вычислить её экспоненту.

	п·Вероятностные распределения
	Одномерные	Многомерные
Дискретные:	Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное	мультиномиальное
Абсолютно непрерывные:	Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma	многомерное нормальное | копула