Распределение Фишера

Распределение Фишера (Распределение Снедекора)

Плотность вероятности
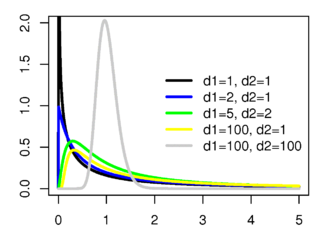
Функция распределения
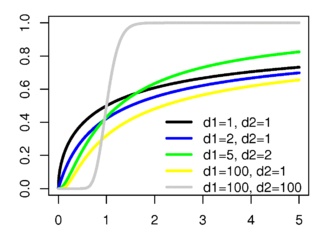
Обозначение	$F(d_1,d_2)\,$
Параметры	$d_1>0,\ d_2>0$ - числа степеней свободы
Носитель	$x \in [0; +\infty)\!$
Плотность вероятности	$\frac{\sqrt{\frac{(d_1\,x)^{d_1}\,\,d_2^{d_2}} {(d_1\,x+d_2)^{d_1+d_2}}}} {x\,\mathrm{B}\!\left(\frac{d_1}{2},\frac{d_2}{2}\right)}\!$
Функция распределения	$I_{\frac{d_1 x}{d_1 x + d_2}}(d_1/2, d_2/2)\!$
Математическое ожидание	$\frac{d_2}{d_2-2}\!$, если $d_2 > 2$
Медиана
Мода	$\frac{d_1-2}{d_1}\;\frac{d_2}{d_2+2}\!$, если $d_1 > 2$
Дисперсия	$\frac{2\,d_2^2\,(d_1+d_2-2)}{d_1 (d_2-2)^2 (d_2-4)}\!$, если $d_2 > 4$
Коэффициент асимметрии	$\frac{(2 d_1 + d_2 - 2) \sqrt{8 (d_2-4)}}{(d_2-6) \sqrt{d_1 (d_1 + d_2 -2)}}\!$, если $d_2 > 6$
Коэффициент эксцесса
Информационная энтропия
Производящая функция моментов	'
Характеристическая функция

Распределе́ние Фи́шера в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений.

Определение

Пусть $Y_1,Y_2$ — две независимые случайные величины, имеющие распределение хи-квадрат: $\,Y_i \sim \chi^2(d_i)$, где $d_i \in \mathbb{N},\; i=1,2$. Тогда распределение случайной величины

$F = \frac{Y_1/d_1}{Y_2/d_2}$,

называется распределением Фишера (распределением Снедекора) со степенями свободы $d_1$ и $d_2$. Пишут $\,F \sim \mathrm{F}(d_1,d_2)$.

Моменты

Математическое ожидание и дисперсия случайной величины, имеющей распределение Фишера, имеют вид:

$\mathbb{M}[F] = \frac{d_2}{d_2 - 2}$, если $d_2 > 2$,

$\mathrm{D}[F] = \frac{2\,d_2^2\,(d_1+d_2-2)}{d_1 (d_2-2)^2 (d_2-4)}\!$, если $d_2 > 4$.

Свойства распределения Фишера

• Если $\,F \sim \mathrm{F}(d_1,d_2)$, то $\, \frac{1}{F} \sim \mathrm{F}(d_2, d_1)$.
• Распределение Фишера сходится к единице. Доказательство:
  если $F_{d_1,d_2} \sim \mathrm{F}(d_1,d_2)$, то $F_{d_1,d_2} \to \delta(x-1)$ по распределению при $d_1,d_2 \to \infty$, где $\delta(x-1)$ — дельта-функция в единице, то есть распределение случайной величины-константы $X \equiv 1$.

Связь с другими распределениями

• Если $F_{d_1,d_2} \sim \mathrm{F}(d_1,d_2)$, то случайные величины $d_1 F_{d_1,d_2}$ сходятся по распределению к $\chi^2(d_1)$ при $d_2 \to \infty$.

	п·Вероятностные распределения
	Одномерные	Многомерные
Дискретные:	Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное	мультиномиальное
Абсолютно непрерывные:	Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma	многомерное нормальное | копула

Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.