Σ-алгебра

σ-алгебра (си́гма-а́лгебра) — это алгебра множеств, замкнутая относительно операции счётного объединения. Сигма-алгебры играют важнейшую роль в теории меры и интегралов Лебега, а также в теории вероятностей.

Определение

Семейство 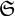$\mathfrak{S}$ подмножеств множества X называется σ-алгеброй, если оно удовлетворяет следующим свойствам:

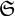1. $\mathfrak{S}$ содержит пустое множество.
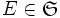2. Если $E\in \mathfrak{S}$, то и его дополнение $X\backslash E\in\mathfrak{S}$.
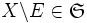3. Объединение счётного подсемейства из 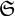$\mathfrak{S}$ также в $\mathfrak{S}$.

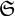Замечания

• Для любой системы множеств 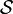$\mathcal{S}$ существует минимальная сигма-алгебра 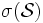$\sigma(\mathcal{S})$, являющаяся её надмножеством.
• Сигма-алгебры являются естественной областью определения счётно-аддитивных мер. Если мера определена частично (на семействе множеств 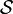$\mathcal{S}$) так, что выполнено условие сигма-аддитивности (синоним счётной аддитивности), эта частичная мера имеет единственное продолжение на 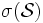$\sigma(\mathcal{S})$, то есть на минимальную сигма-алгебру, это семейство содержащую, и при этом свойство сигма-аддитивности не нарушится.
• σ-алгебра, порождённая случайной величиной 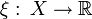$\xi:\,X\rightarrow \mathbb{R}$, определяется следующим образом:

$\sigma(\xi) = \left\{\xi^{-1}(B)\mid B \in \mathcal{B}(\mathbb{R})\right\}$,

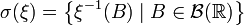где 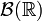$\mathcal{B}(\mathbb{R})$ — борелевская сигма-алгебра на вещественной прямой. Это — минимальная сигма-алгебра на пространстве X, относительно которой случайная величина ξ всё ещё остаётся измеримой. Эта же конструкция применяется и в том случае, если на пространстве X вообще не выделена никакая сигма-алгебра, в этом случае с помощью функции ξ её можно ввести и наделить таким образом пространство X структурой измеримого пространства так, что функция ξ будет измеримой.

Связанные определения

• Измеримое пространство — это пара 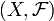$(X, \mathcal F)$, где X — множество, а 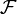$\mathcal F$ — сигма-алгебра его подмножеств.

Примеры

• Борелевская сигма-алгебра
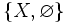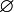• Для любого множества X можно построить тривиа́льную σ-алгебру $\{X,\varnothing\}$, где $\varnothing$ — пустое множество.
• Для любого множества X можно построить ещё одну тривиа́льную σ-алгебру, которая содержит все его подмножества.