АЛГЕБРА ЛОГИКИ

АЛГЕБРА ЛОГИКИ

        система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова — алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются логические операции над высказываниями, каждое из которых имеет одно из двух значений истинности: «истина» (сокр. «и» или 1) и «ложь» («л» или 0). Элементами А. л. служат переменные, принимающие одно из этих двух значений, а также константы 1 и 0. Предмет А. л. составляет совокупность свойств логич. операций в этой двузначной алгебре, а также вытекающие из этих свойств правила преобразования и упрощения формул А. л. (интерпретируемых как высказывания) и приведения их к некоторым стандартным формам, пригодным для алгоритмизации (см. Алгоритм) решения логич. задач. А. л. в широком смысле включает распространение методов А. л. на понятия и задачи многозначной логики: вместо теории двузначных арифметич. функций от двух аргументов в n-значной логике рассматриваются nзначные функции от аргументов О, 1, ..., n — 1, причём часть из этих значений, подобно истинному значению 1 в двузначной А. л., считается «выделенными», т. е. соответствующими «истине». Термин «А. л.», идущий от традиций первых работ по математич. логике 19 в. (Дж. Буль, У. С. Джевонс, Э. Шредер, П. С. Порецкий и др.), применяют иногда также в другом, расширит, смысле к алгебраич. задачам и методам логики предикатов, составляющим предмет теории моделей.

        Гильберт Д., Аккерман В., Основы теоретич. логики, пер. с нем., М., 1947; Клини С. К., Математич. логика, пер. с англ., М., 1973.

Философский энциклопедический словарь. — М.: Советская энциклопедия. Гл. редакция: Л. Ф. Ильичёв, П. Н. Федосеев, С. М. Ковалёв, В. Г. Панов. 1983.

А́ЛГЕБРА ЛО́ГИКИ

одна из осн. частей математич. логики, основанная на применении алгебраич. методов к логике. Возникнув в сер. 19 в. в трудах Буля и развиваясь затем в работах Джевонса, Шрёдера;, Пирса, Порецкого и др., А. л. имела своим предметом классы (как объемы понятий), соотношения между ними по объему и связанные с этим операции над ними. Само создание А. л. представляло собой попытку решать традиц. логич. задачи алгебраич. (т.е. характерными для алгебры) методами. В связи с появлением в 70-х гг. 19 в. теории множеств (см. Множеств теория), поглотившей часть прежнего предмета А. л. (теоретико-множеств. операции), и дальнейшим развитием математич. логики в трудах Фреге, Рассела, Гильберта и др. (последняя четверть 19 в. и 1-я пол. 20 в.; для развития А. л. большое значение имели труды И. И. Жегалкина) предмет А. л. значительно изменился. Основным ее предметом, особенно в работах сов. ученых, являются высказывания (объекты, родств. предложениям, суждения и т.п.), рассматриваемые со стороны их логич. значений (истина, ложь, бессмыслица и т.п.), и те логич. операции над ними, для изучения к-рых достаточно иметь дело лишь с этой стороной высказываний.

Наличие у А. л. этого предмета, изучаемого не только алгебраич. методами, а также связь самих алгебраич. методов с иными математич. методами порождают многочисл. связи А. л. с другими разделами математич. логики (исчисления высказываний, исчисления классов, исчисления предикатов, теория функций алгебры логики, логико-математич. теория релейно-контактных схем и др.). Этим же обусловливается и нек-рое проникновение в А. л. таких методов, как аксиоматич. метод, методы теории алгоритмов, теории множеств (см. Теоретико-множественная логика), топологии и др.

Роль спец. методов в логике (в частности, математич. методов, без к-рых нет и не может быть математич. логики), как и в др. науках, состоит в том, что они позволяют найти новые способы подхода к изучаемому предмету, выявить новые стороны его, важность к-рых подтверждается практикой. Так, в частности, А. л., использующая в своей основе далеко идущие абстракции, огрубление и формализацию, находит все более широкое применение в технике (особенно при решении задач, связанных с построением автоматов) и, наоборот, развивается сама под влиянием запросов техники (задач автоматизации программирования, уменьшения числа элементов в устройствах релейного действия и др.).

В основе обычной, т.н. классич. А. л. лежит абстракция высказывания как величины, имеющей одно (и только одно!) из двух значений: "истина" или "ложь" (короче: И, Л), или могущей принимать оба эти значения (но не одновременно). В первом из этих случаев имеем индивидуальное высказывание (высказывание в узком, наиболее принятом смысле этого слова), во втором – высказывание-функцию. Примеры высказываний: "2 · 2 = 4", "0 ≤ 0", "Сократ – человек", "0 = 1", "2 · 2 = 5", "х² = у", "z – человек", "Если х = у, то у = 0", "Если х = 2, то х² = 4", "х равняется у или х не равняется у". Первые три высказывания имеют значение И (т.е. истинны), 4-е и 5-е – значение Л (т.е. ложны), 6-е, 7-е, 8-е – высказывания-функции (если, напр., значениями буквенных переменных х и у могут быть целые числа, а переменной z – живые существа), 9-е и 10-е имеют значение И (при всех возможных значениях переменных х и у). Последние три из этих высказываний являются сложными, в отличие от предшествующих им простых. При этом высказывание наз. сложным, если в нем есть хотя бы одна из связок "и", "или", "если..., то", "эквивалентно" и т.п. или частица "не". Абстракция в А. л. идет дальше рассмотрения значений высказываний. Именно, все истинные высказывания отождествляются между собой, т.к. истинное высказывание не отличается от другого истинного высказывания по значению (от других сторон высказываний в А. л. отвлекаются). Ложные высказывания между собой тоже отождествляются. При рассмотрении же высказываний-функций в А. л. обычно отвлекаются от рассмотрения зависимости их от иных переменных, кроме таких, значениями к-рых являются тоже высказывания, вводя для их рассмотрения буквенные переменные, к-рые мы будем называть переменными высказываниями (точнее, переменными для высказываний). Таковыми являются буквы А, В, С,..., А1, А2, А3,... и т.п. (не обязательно именно заглавные латинские; выбор последних – вопрос не существа А. л., а соглашения) при условии, что они играют роль переменных, значениями к-рых могут быть всевозможные индивидуальные высказывания, т.е., в силу упомянутых абстракций, "константы" И и Л. Буквенные обозначения высказываний вообще характерны для А. л. подобно тому, как для обычной школьной алгебры характерны буквенные обозначения чисел. Так, не только переменные высказывания, но и индивидуальные часто обозначаются буквами А, В, С и т.п. (но играющими при этом роль констант).

Кроме простых высказываний, обозначаемых отд. буквами А, В... или И, Л, рассматриваются также сложные высказывания – результат соединения высказываний связками или отрицания их (соответствующего частице "не"). Сложные высказывания рассматривают как функции от входящих в них буквенных переменных А, В, С и т.д. Так появляется понятие функции А. л. - функции от аргументов, являющихся переменными высказываниями, т.е. принимающих значения И, Л, к-рая (функция) может принимать тоже лишь эти значения. Для сложных высказываний в связи с этим часто употребляются функциональные обозначения ƒ (A), D (В), Φ (А, В, С), ψ (А1, А2,...,An) и т.п.

Однако более систематич. употребление находят в А. л. другие обозначения - обозначения алгебраич. операций над высказываниями. Эти операции, играющие в А. л. роль, аналогичную той, к-рую в обычной школьной алгебре играют операции сложения, вычитания, умножения и др. операции над числами, соответствуют в А. л. упомянутым выше связкам и частице "не". Так вводятся операции: конъюнкция А В (читается "А и В"; другие обозначения: AB, A & B, А / В; другие названия: логическое умножение, булево умножение), дизъюнкция A / B (чит. "А или В"; другие обозначения: А + В, АВ; другие названия: логическое сложение, булево сложение), импликация А → В (чит.: "Если А, то В" или "А влечет В", или "А имплицирует В", или "Из А следует В"; другие обозначения: A з B; другое название: логическое следование), эквиваленция А А́ЛГЕБРА ЛО́ГИКИ В (чит.: "А эквивалентно В" или "А равнозначно В", или "А, если и только если В"; другие обозначения: А =В, А < — > В, А Z В, А = В; другие названия: эквивалентность, равнозначность, равносильность), отрицание Ā (чит.: "не А", или "А ложно", или "не верно, что А", или "отрицание А"; другие обозначения: → А, А́ЛГЕБРА ЛО́ГИКИ А, А'; другое название: инверсия), а также иногда и др. операции.

Одной из важных сторон формализации, принимаемой в А. л., является то, что знаками этих операции (т.е. по смыслу, соответствующими им связками) можно соединять любые высказывания, без ограничения, в т.ч. и те, к-рые сами являются сложными. Так возникают такие выражения (символич. высказывания), как

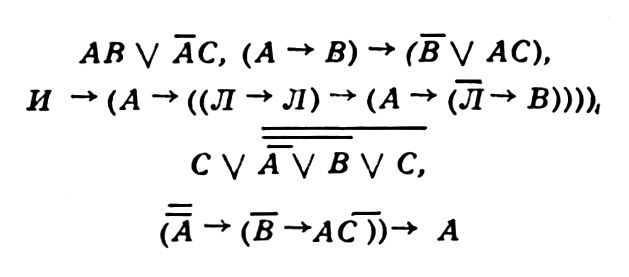и т.п., а также, вместе с ними, такие, казалось бы, противоестественные конструкции, как высказывания "Если 2 · 2 = 5, то все люди верблюды", "Если 0 = 1, то: если 0 = 1, то 1 = 1 и 1 < 3" и т.п. Нек-рые из получающихся выражений, как, напр., (((А / В) С / D) E / AF) (AB / EF), даже трудно словесно высказать и приходится читать путем перечисления всех знаков, включая скобки. Зато при этом удается точно и строго описать класс всех рассматриваемых выражений А. л. В данном случае он состоит из констант И и Л, переменных А, В... и всех тех выражений, к-рые получаются из них путем конечного числа соединений знаками "·", "/", "→" и "А́ЛГЕБРА ЛО́ГИКИ" и отрицаний. В др. случаях рассматриваются др. классы выражений, содержащие др. знаки операций или же только эти, но не все из них.

Такие же неудобочитаемые выражения, как вышеприведенное, вовсе не являются "мертвым грузом" в А. л. Они могут наряду с др. выражениями получаться, напр., при анализе релейно-контактных схем или в результате преобразований других, более удобочитаемых, но громоздких выражений, что применяется, напр., при синтезе контактных схем. Да и необычность приведенных выше "противоестественных" высказываний можно усмотреть, лишь выйдя за рамки А. л., в к-рой они, наоборот, приобретают вполне определ. смысл и, не отличаясь ничем от высказываний, соответственно, А → В и С → (С → DE) при А = В = С = Л и D = Е = И, являются даже истинными.

Это связано с др. важной стороной формализации в А. л. – требованием, чтобы операции задавались таблично как функции, т.е. чтобы значение сложного высказывания зависело только от значений составляющих его простых высказываний. Так, конъюнкция задается таблицей: И · И = И, И · Л = Л, Л · Л = Л, Л · Л = Л; дизъюнкция – таблицей: И / И = И, И / Л = И, Л / И = И, Л / Л = Л; импликация – таблицей: И → И = И, И → Л = Л, Л → И = И, Л → Л = И (эта таблица вытекает из требования табличное операции и естеств. требований, чтобы были такие случаи, когда А → В ложно, но чтобы все частные случаи такого высказывания, как "Если х = 2, то х2 = 4", были истинны; случаи, когда х принимает одно из значений 2,–2,1, как раз и дают три из четырех равенств таблицы); эквиваленция – таблицей: И А́ЛГЕБРА ЛО́ГИКИ И = И, И А́ЛГЕБРА ЛО́ГИКИ Л = Л, Л А́ЛГЕБРА ЛО́ГИКИ И = Л, Л А́ЛГЕБРА ЛО́ГИКИ Л = И; отрицание – таблицей: И = Л, Л = И. Эти таблицы позволяют вычислять значения сложных высказываний, зная значения простых.

Осн. суть А. л. как системы методов состоит в использовании преобразований высказываний на основе тех алгебраич. законов, к-рые имеют место для операций над высказываниями. Эти законы чаще всего имеют вид тождеств, т.е. равенств, верных при всех значениях переменных.

Важную роль играют следующие тождества:

I. AB = ΒΑ, Α / В = В / А

(законы коммутативности);

II. (АВ)С = А (ВС), (А / В) / С = А / (В / С)

(законы ассоциативности);

III. А(А / В) = А, А / AB = А

(законы поглощения);

IV. А (В / С) = AB / АС

(закон дистрибутивности);

V. АĀ = Л

(закон противоречия);

VI. А / Ā = И

(закон исключенного третьего).

Эти тождества, устанавливаемые, напр., с помощью таблиц, позволяют уже без помощи таблиц получать др. тождества. При этом методом получения последних является метод тождеств. преобразований (т.е. преобразований, к-рые, изменяя выражение, не изменяют при этом функцию, выражаемую последним), совершенно аналогичных тем, которые изучаются в школьном курсе алгебры (но основанных уже на новых тождествах).

Так получим, напр., законы идемпотентности; АА = А, А / А = А [последний доказывается так:

А / А = А / А (А / B) = A,

т.е. с использованием лишь (обоих) законов поглощения]; 2-й закон дистрибутивности A / BC = (А / B) (А / C) [доказательство: A / ВС = А / АС / ВС = А / СА / СВ = А(А / B) / C(A / B) = (A / B)A / (A / B)C = (A / B) (A /C)]; двойного отрицания закон

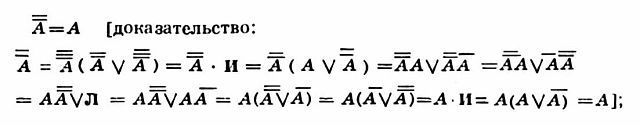законы де Моргана:

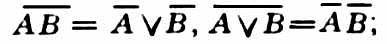законы зачеркивания:

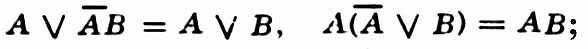законы выявления:

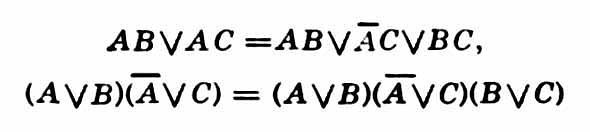Вообще тождеств I-VI достаточно для того, чтобы из них по методу тождеств. преобразований можно было вывести всякое (верное, конечно) тождество, левая и правая части к-рого – выражения А. л., состоящие из переменных А, В,..., констант И, Л и знаков"·", "/", "–" (не обязательно включая все из них). Добавление же тождеств VII A → B = Ā / B, А А́ЛГЕБРА ЛО́ГИКИ В = АВ / ĀВ дает возможность выводить и любые тождества, содержащие также знаки "→", "А́ЛГЕБРА ЛО́ГИКИ". Напр., такие: А → (В → С) = АВ → С (закон объединения посылок), А (А → В) = AB (закон зачеркивания посылки), Ā → В = В →А (закон контрапозиции) Ā А́ЛГЕБРА ЛО́ГИКИ В = А А́ЛГЕБРА ЛО́ГИКИ В (закон четности эквиваленции), А → А= И, А А́ЛГЕБРА ЛО́ГИКИ А = И, А → Ā = Ā, А А́ЛГЕБРА ЛО́ГИКИ Ā = Л, А А́ЛГЕБРА ЛО́ГИКИ В = (А → В). (В → А), А / (В А́ЛГЕБРА ЛО́ГИКИ С) = (A / B) А́ЛГЕБРА ЛО́ГИКИ (A / C) и др. Использование перечисл. тождеств позволяет уже без большого труда выводить и многочисл. гораздо более сложные тождества, например (A →(B →(C →(D → E)))) → (A →(B →(C →(D → F)))) = (A →(B →(C →(E → F)))), (Ā А́ЛГЕБРА ЛО́ГИКИ B) →((C А́ЛГЕБРА ЛО́ГИКИ D) →(E А́ЛГЕБРА ЛО́ГИКИ (F А́ЛГЕБРА ЛО́ГИКИ G))) = (A А́ЛГЕБРА ЛО́ГИКИ B)(C А́ЛГЕБРА ЛО́ГИКИ D) → (E А́ЛГЕБРА ЛО́ГИКИ (F А́ЛГЕБРА ЛО́ГИКИ G)), AB / AC / BC / DE / DF / EF / ĀD / BĒ / CF = И, проверять к-рые непосредственно по таблицам было бы уже довольно трудно.

В записи последнего из этих тождеств существ. роль играет использование закона ассоциативности дизъюнкции, к-рый позволяет обходиться без скобок при записи выражения, к-рое можно понимать как дизъюнкцию неск. выражений (членов), т.е. такую же роль, какую в обычной школьной алгебре играет закон ассоциативности сложения (сочетательный закон) при записи суммы неск. слагаемых. Аналогичное можно сказать и о законе ассоциативности конъюнкции. Можно вывести также закон ассоциативности эквивалентности. Однако связанное с ним понятие эквиваленции нескольких переменных надо не путать с (попарной) эквивалентностью их. Так, А А́ЛГЕБРА ЛО́ГИКИ В А́ЛГЕБРА ЛО́ГИКИ С [т.е. (А А́ЛГЕБРА ЛО́ГИКИ В) А́ЛГЕБРА ЛО́ГИКИ С] и (А А́ЛГЕБРА ЛО́ГИКИ В) (В А́ЛГЕБРА ЛО́ГИКИ С) [т.е. попарная эквивалентность] выражают различные функции [напр., Л А́ЛГЕБРА ЛО́ГИКИ Л А́ЛГЕБРА ЛО́ГИКИ Л = (Л А́ЛГЕБРА ЛО́ГИКИ Л) А́ЛГЕБРА ЛО́ГИКИ Л = И А́ЛГЕБРА ЛО́ГИКИ Л = Л, но (Л А́ЛГЕБРА ЛО́ГИКИ Л) (Л А́ЛГЕБРА ЛО́ГИКИ Л) = И · И = И]. Здесь сказывается различие между операцией эквиваленции и отношением эквивалентности, хотя это, казалось бы, и одно и то же. Тем более следует соблюдать осторожность при сопоставлении эквиваленции неск. выражений, напр. U А́ЛГЕБРА ЛО́ГИКИ B А́ЛГЕБРА ЛО́ГИКИ G,с их равенством U = B = G, т.к. последнее означает именно попарное равенство (U = B и B = G); необходимо либо строго различать эквиваленцию и равенство, либо, в случае их отождествления, избегать, напр., опускания скобок по ассоциативности.

Тождества V, VI, VII показывают, что константы И и Л, импликацию и эквиваленцию, рассматривая их как функции, можно выразить через конъюнкцию, дизъюнкцию и отрицание. Более того, имеет место теорема, гласящая, что всякая функция А. л. может быть представлена через эти три операции, т.е. записана в виде выражения, содержащего лишь знаки этих операций и буквенные переменные. Именно, любую функцию Φ (А1, А2,...,An) можно записать как дизъюнкцию всех выражений вида Ф (а1, а2,..., аn) · (А1 А́ЛГЕБРА ЛО́ГИКИ а2) (А2 А́ЛГЕБРА ЛО́ГИКИ а2)(Аn А́ЛГЕБРА ЛО́ГИКИ аn),

где а1, а2,..., аn – набор из значений И, Л. Заменяя в этой дизъюнкции выражения Аi А́ЛГЕБРА ЛО́ГИКИ И на Аi, а Аi А́ЛГЕБРА ЛО́ГИКИ Л – на Аi, a также стирая "коэффициенты" Ф(а1, а2,..., аn), равные И (по закону И · А = А) и отбрасывая члены с "коэффициентами", равными Л (по законам (Л · А = Л, Л / А = А), мы и получим (если функция не есть константа) то выражение, о к-ром говорится в теореме. Последнее наз. совершенной дизъюнктивной нормальной формой функции Ф(А1,...,An).

Дизъюнктивной нормальной формой (короче, днф) наз. выражение, к-рое есть буква И или Л или имеет вид U1 / U2 /.../ Us где каждый член Ui является либо буквенной переменной, либо ее отрицанием, либо конъюнкцией таковых, причем s не обязательно отлично от 1, т.е. знаков "/" может и не быть. Примеры днф: А, B, ĀBC, AB / С, АĀ / СС, АВАС / BСВ, ĀBCD / A / D / CE, ABCD / ABCD / ĀBCD, И, Л. Последние из этих днф являются т.н. совершенными. Днф наз. совершенной, если она есть И или Л или в каждом члене содержит ровно по одному разу все имеющиеся в ней буквы (переменные) и не имеет одинаковых членов. (Два выражения наз. одинаковыми, если одно из другого можно получить с помощью одних лишь законов коммутативности и ассоциативности). Всякое выражение А. л. можно привести (преобразовать) к днф. Для этого достаточно элиминировать (т.е. исключить) константы и знаки операций, отличных от конъюнкции, дизъюнкции и отрицания, выразив их через эти операции (напр., по V, VI, VII), а затем "спустить внутрь" (по законам де Моргана) все знаки отрицания, стоящие над сложными высказываниями, ликвидировать кратные отрицания (по закону А = А) и, наконец, раскрыть все скобки по закону дистрибутивности (при использовании также законов ассоциативности и коммутативности). А всякую днф можно привести к совершенной днф, "домножая" члены на недостающие буквы (по закону А = АВ / АB) и ликвидируя повторения букв в членах (по законам АА = А, АĀ = Л, Л · А = Л Л / А = А) и повторения членов (по закону А / А=А).

Приведение к совершенной днф лежит в основе одного из алгоритмов для решения по любым двум данным выражениям U и B вопроса о том, одну ли и ту же функцию они выражают, т.е. верно ли тождество U = B. Алгоритм этот состоит в следующем: приводим U и B к совершенным днф, содержащим все те переменные, к-рые есть в U, и все те, к-рые есть в U, и смотрим, одинаковы ли эти две совершенные днф; если одинаковы, то ответ положителен, если нет – отрицателен. Однако совершенная днф, находя применение и к др. задачам, является все же часто весьма громоздкой. Поэтому приходится нередко пользоваться др. нормальными формами.

Из них важную роль играет т.н. сокращенная днф. Последнюю можно определить как такую днф, в к-рой 1) нет повторений букв ни в одном члене, 2) нет таких пар членов Ui; и Uj, что всякий множитель из Ui имеется и в Uj, и 3) для всяких двух таких членов, из к-рых один содержит множителем нек-рую букву, а другой – отрицание той же буквы (при условии, что другой буквы, для к-рой это же имеет место, в данной паре членов нет), имеется (в этой же днф) член, равный конъюнкции остальных множителей этих двух членов. Всякую днф можно привести к сокращенной днф путем конечного числа выбрасываний членов по закону поглощения (ср. с условием 2) и добавлений членов по закону выявления (ср. с условием 3) с использованием также нек-рых более простых законов (коммутативность, ассоциативность, А = А · И) и ликвидацией повторений букв в членах и повторений членов. Пример приведения выражения к сокращенной днф:

Тождество U = B верно, если, и только если, получаемые из U и B сокращенные днф одинаковы.

Кроме днф, употребляются также конъюнктивные нормальные формы (кнф). Это такие выражения, к-рые можно получить из днф путем замены в них знаков "/" на "·", а "·" на "/". [Пример кнф А(В / C / D)(A / D)]. Конечно, такое преобразование не является тождественным, т.е. может изменить функцию, выражаемую данной днф. Оно есть преобразование двойственности.

Преобразованием двойственности наз. такое преобразование выражения А. л., при к-ром в этом выражении знаки всех операций заменяются на знаки двойственных им операций, а константы: И на Л, Л на И; причем операция (или функция) Ф наз. двойственной для операции ψ, если таблица, задающая Ф, получается из таблицы, задающей ψ, путем замены в ней всюду И на Л, а Л на И (имеется в виду одновременная замена и значений функции, и значений ее аргументов). Если Φ двойственная ψ, a ψ двойственная χ, то Φ = χ. Напр., конъюнкция и дизъюнкция двойственны между собой, отрицание двойственно самому себе, константа И (как функция) двойственна константе Л. Функция Ф(А1, Аn) двойственна функции ψ (А1, Аn), если, и только если, верно тождество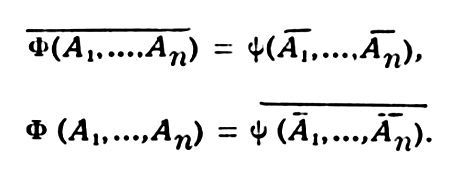

Если верно тождество U = B и U* двойственно U, а B* двойственно B, то верно и тождество U* = B*, называемое двойственным предыдущему тождеству. Это – т.н. принцип двойственности. Примерами двойственных тождеств являются пары законов Ι, ΙI, III и др.; тождество V двойственно тождеству VI.

Совершенную кнф и сокращенную кнф можно определить как такие кнф, что двойственные им выражения есть, соответственно, совершенная днф и сокращенная днф. Совершенные и сокращенные днф и кнф можно использовать для решения задачи обзора всех гипотез и всех следствий данного выражения А. л. Причем под гипотезой выражения U А. л., т.е. в условиях принятых в ней абстракций, естественно понимать такое выражение B, что B → U тождественно истинно, т.е. истинно при всех значениях переменных высказываний; а под следствием выражения U – такое выражение B, что U → B тождественно истинно. Гипотеза выражения U наз. простой, если она есть конъюнкция буквенных переменных или их отрицаний и после отбрасывания какого бы то ни было из этих ее множителей перестает быть гипотезой выражения U. Аналогично, следствие выражения U наз. простым, если оно есть дизъюнкция букв или их отрицаний и после отбрасывания какого бы то ни было из ее членов перестает быть следствием выражения U. Решение задач обзора гипотез и следствий основано на следующих теоремах. 1°. Если U = B, то у U и у B одни и те же гипотезы и одни и те же следствия. 2°. Каждый член днф является гипотезой этой днф. 3°. Каждый множитель кнф есть следствие этой кнф. 4°. Если B – гипотеза выражения U, то BG – тоже гипотеза выражения U. 5°. Если B – следствие выражения U, то B / G – тоже следствие выражения U. 6°. Если B и G – гипотезы выражения B, то B / G – тоже гипотеза выражения U. 7°. Если B и G – следствия выражения U, то BG – тоже следствие выражения U. 8°. У совершенной днф нет других гипотез (не содержащих букв, не входящих в эту днф), кроме дизъюнкций (нек-рых) ее членов или тождественно равных им (т.е. равных при всех значениях переменных) выражений. 9°. У совершенной кнф нет других следствий, кроме конъюнкций (нек-рых) ее множителей или тождественно равных им выражений. 10°. Сокращенная днф есть дизъюнкция всех своих простых гипотез. 11°. Сокращенная кнф есть конъюнкция всех своих простых следствий. Из обзора же простых гипотез и следствий нетрудно получить (пользуясь 2°–7°) и обзор всех остальных гипотез и следствий.

Такие уже встречавшиеся выше словесные выражения, как "множитель члена днф", "множители совершенной кнф" и т.п., становятся еще более понятными и оправданными после совершения еще одного, часто употребляемого в А. л. шага абстракции. Последний состоит в отождествлении И с числом 1, а Л – с числом 0. Это еще больше сближает А. л. с обычной школьной алгеброй и арифметикой. Таблица конъюнкции при этом приобретает следующий вид; 0 · 0 = 0, 0 · 1 = 0, 1 · 0 = 0, 1 · 1 = 1, т.е. конъюнкция становится обычным умножением в области чисел 0 и 1. Вводится еще одна операция А + В, задаваемая таблицей: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 0. Она наз. сложением (точнее сложением по модулю 2; др. назв.: разделительная дизъюнкция; читается: "А плюс В", или "А не эквивалентно В", или "Либо А, либо В").

Всякую функцию А. л. можно представить через умножение (т.е. конъюнкцию), сложение и константу 1 (теорема Жегалкина). В частности, верны следующие тождества:

VIII. А / В = AB + А + В, Ā = А + 1

IX. А → В = AB + А + 1, А А́ЛГЕБРА ЛО́ГИКИ В = А + В + 1.

Обратные представления имеют вид:

X. A + B = AВ / ĀB, l = A / Ā.

Тождества VIII позволяют "переводить" выражения "языка" конъюнкции, дизъюнкции и отрицания (КДО) на "язык" умножения, сложения и единицы (УСЕ), а тождества X – осуществлять обратный "перевод". Только "переводы" эти таковы, что "переведя" по этим тождествам выражение с первого языка на второй, а то, что получится, обратно на первый, мы, как правило, получим не то выражение, из к-рого исходили, а более сложное, хотя, во всяком случае, и тождественно равное ему; пример:

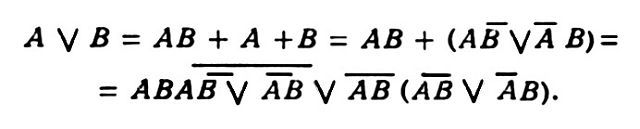Тождеств. преобразования можно производить и на "языке" УСЕ, что даже гораздо удобнее, чем на "языке" КДО, т.к. они при этом гораздо более похожи на те, к-рые привычны для всех, знающих школьную алгебру. В основе их лежат следующие тождества:

I. АВ =ВА, А + В = В + А

(законы коммутативности);

XII. (AB)С = А(ВС), (А + В) + С = А + (В + С)

(законы ассоциативности);

XIII. А (В + С) = AB + AC

(закон дистрибутивности);

XIV. АА = А, А + (В + В) = А

XV. А · 1 = А.

Этих тождеств достаточно для того, чтобы из них по методу тождеств, преобразований можно было вывести любое (верное) тождество, обе части к-рого суть выражения "языка" УСЕ. А добавив к ним тождества VIII, мы сможем выводить и все тождества "языка" КДО.

Выражение "языка" УСЕ наз. приведенным полиномом (п.п.), если оно есть 1 + 1 (т.е. нуль) или имеет вид U1 + U2 +...+ Us где каждый член Ui есть либо 1, либо буквенная переменная, либо произведение последних, причем ни в одном члене нет никаких повторений букв, никакие два члена не одинаковы (в том же смысле, что и выше), a s не обязательно больше 1 (т.е. знаков "+"может не быть). Примеры п.п.: 1, 1 + 1, А, В, А + В + 1, ABC, А + АВ + В + ВСD, ABD + BCD + CD + CE + 1.

Всякое выражение А. л. можно привести к п. п. (теорема Жегалкина). Для этого достаточно элиминировать в данном выражении 0 и знаки операций, отличные от "·" и "+", "переводя" их на "язык" УСЕ, а затем раскрыть скобки (по закону дистрибутивности, с использованием также, здесь и дальше, законов коммутативности и ассоциативности) и ликвидировать повторения букв в членах (по закону АА = А) и повторения членов (по законам А + В + В = А, А + А = 1 + 1). Тождество U = B верно, если, и только если, U и B приводятся к одинаковым п.п.

Кроме "языков" КДО и УСЕ, существуют и др. "языки", равносильные им в том смысле, что всякое выражение первых переводимо на последние и обратно (в этом смысле КДО и УСЕ тоже равносильны между собой). В основу такого "языка" достаточно положить любую систему операций (и констант), обладающую тем свойством, что через операции (и константы) этой системы можно представить всякую функцию А. л. Такие системы наз. (функционально) полными (см. Полнота функциональная).

Примеры полных систем: а) конъюнкция и отрицание (примеры представлений:

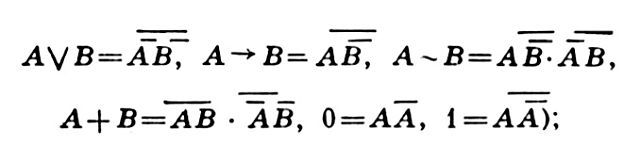б) дизъюнкция и отрицание (примеры представлений – тождества, двойственные предыдущим); в) импликация и отрицание [примеры представлений:

АВ = А → В, A / B = A → B, А + В = (А → В) → В → А, 0 = A → A, 1 = A → A);

г) импликация и 0 [примеры представлений:

АВ = (A → (B →0)) → 0, A / B = (A → B) → B, A = A → 0, 1 = 0 → 0];

д) умножение, эквиваленция и 0 [примеры представлений:

А / В = AB А́ЛГЕБРА ЛО́ГИКИ A А́ЛГЕБРА ЛО́ГИКИ B, А → В = АВ А́ЛГЕБРА ЛО́ГИКИ А, А = А А́ЛГЕБРА ЛО́ГИКИ 0, 1 = 0 А́ЛГЕБРА ЛО́ГИКИ 0];

е) штрих Шеффера А|В [определение: A|B = AB; примеры представлений:

АВ = (A|B)|(A|B), A / B = (A|A)|(B|B), A → B = (A|B)|A, A=A|A, A + B = ((А|В)|А)|(A|В)|В), 1 = (А|А)|А)];

ж) медиана (А, В, С), отрицание и 1 [определение: (А, В, С) = АВ / АС / ВС; примеры представлений: АВ = (А, В, 1), А / B = (А, В, 1), А → В = (А, В, 1), А А́ЛГЕБРА ЛО́ГИКИ В = (A, B, 1),(A, B, 1),1) 0 = 1];

и) медиана, эквиваленция и сложение [примеры представлений:

0 = А + А, 1 = А А́ЛГЕБРА ЛО́ГИКИ А, А = А А́ЛГЕБРА ЛО́ГИКИ (А + A) АВ = (А, В, А + А), A / B = (A, В, А А́ЛГЕБРА ЛО́ГИКИ А)].

Заметим, что для медианы имеет место ряд своеобразных тождеств; например (А, А, В) = А, (А, A, В) = В, (А, B, С) = (А, В, С) (закон самодвойственности), (А, В, С) = (В, С, А) = (А, С, В) (законы симметричности). (А, В, С) + D = (A + D, B + D, С + D) (закон дистрибутивности сложения относительно медианы), ((А, В , С), D, E) = ((A, D, E), (B, D, E), (С, D, E)) (закон самодистрибутивности). ((А, В, С), D, А) = (А, В, (С, D, А)) (закон частичной ассоциативности) и др.

Можно, очевидно, строить и такие "языки", в основе к-рых лежат системы операции, не являющиеся полными (напр. конъюнкция и дизъюнкция, сложение и отрицание, медиана и отрицание, медиана и сложение, импликация и конъюнкция, отрицание и константы). Если рассматривать не только те операции, к-рые встречались выше, но вообще всевозможные операции А. л., допускающие табличное задание (т.е., по существу, всевозможные функции А. л.), то таких "языков" можно построить бесконечно много. Среди них даже найдется бесконечно много попарно неравносильных "языков" (в смысле отсутствия взаимной "переводимости" с одного "языка" на другой). Однако для всякого "языка", построенного на основе тех или иных операций А. л., существует такая конечная система тождеств этого "языка", что всякое тождество этого "языка" выводимо по методу тождеств. преобразований из тождеств этой системы (теорема Линдона). Такая система тождеств наз. (дедуктивно) полной системой тождеств (п.с.т.) данного "языка" (см. Полнота дедуктивная). Напр., тождества I–VI составляют п. с. т. "языка" КДО (если считать, что константы И и Л тоже входят в этот "язык"); тождества XI–XV – п.с.т. "языка" УСЕ, тождества I–IV – п.с.т. "языка" конъюнкции и дизъюнкции, тождества XI–XIV – п.с.т. "языка" умножения и сложения, тождества I–VII – п.с. т. "языка" конъюнкции, дизъюнкции, отрицания, импликации и эквиваленции. Впрочем, последний "язык" мало отличается от "языка" КДО из-за того, что импликация и эквиваленции могут быть в нем элиминированы (по тождествам VII).

Иногда совершают еще один важный дальнейший шаг абстракции. Он состоит в том, что, рассматривая тот или иной из упомянутых выше "языков" вместе с нек-рой п. с. т. этого "языка" отвлекаются от табличного задания операций, лежащих в основе этого "языка", и от того, что значениями его буквенных переменных являются высказывания. Вместо этого допускаются различные интерпретации рассматриваемого "языка", состоящие из той или иной совокупности объектов (служащих значениями буквенных переменных) и системы операций над объектами этого множества, удовлетворяющих тождествам из п. с. т. этого "языка".

"Язык" КДО в результате такого шага абстракции превращается в "язык" т.н. булевой алгебры, "язык" УСЕ – в "язык" т.н. булева кольца (с единицей), "язык" конъюнкции и дизъюнкции – в "язык" т.н. дистрибутивной структуры. Булевой алгеброй наз. любая совокупность элементов (объектов), среди к-рых выделены два элемента, обозначенные соответственно: 0 и 1, и в применение к любым элементам к-рой определены операции AB, A / B и Ā, удовлетворяющие тождествам I–VI (если Л в V заменить на 0, а И в VI – на 1; вместо знака "/" в "языке" булевой алгебры чаще употребляют знак "+"). Аналогично определяются понятия булева кольца, дистрибутивной структуры, структуры (последнее связывается с тождествами I–III).

Важным примером булевой алгебры является алгебра классов, в к-рой роль элементов играют подмножества (классы) нек-рого фиксированного множества (т. н. универсума) U, роль 0 – пустое множество Λ, роль 1 – само U, роль AB, A / B и Ā – теоретико-множеств. операции пересечения, объединения и дополнения, соответственно.

Пересечением множеств А и В наз. их общая часть, т.е. множество всех элементов, принадлежащих и А и В одновременно; объединением множеств А и В наз. множество всех элементов, принадлежащих А или В; дополнением множества А наз. множество всех элементов универсума, не принадлежащих А. Другим примером булевой алгебры является алгебра предикатов (определенных на нек-рой области предметов, тоже играющей роль универсума), в к-рой роль 0 играет тождественно ложный предикат (т.е. ложный при всех значениях своих аргументов), роль 1 – тождественно истинный предикат, роль AB, A / B и Ā – так же, как и в случае обычной алгебры высказываний, – конъюнкция, дизъюнкция и отрицание, соответственно. Связь между алгеброй классов, алгеброй предикатов и алгеброй высказываний, этими тремя важнейшими интерпретациями абстрактной А. л. – "языка" булевой алгебры, состоит в следующем: первая переходит во вторую путем замены множеств (классов) их т.н. характеристическими предикатами (т.е. множества А – предикатом (х∈А, гласящим: "х принадлежит множеству А"), если при этом соответствующим образом преобразуются также операции и константы 0 и 1, а вторая переходит в третью при подстановке во все предикаты на место их аргументов нек-рого фиксированного их значения. Вернее, при таком переходе от алгебры классов к алгебре предикатов получается алгебра не всех предикатов (определенных на универсуме), а лишь алгебра одноместных предикатов – частный случай алгебры предикатов. Другим важным частным случаем последней является алгебра двуместных предикатов, называемых чаще отношениями. С ней тесно связана т.н. алгебра отношений, отличающаяся от нее только тем, что в последней, кроме трех операций булевой алгебры, имеются еще две операции.

Всякую булеву алгебру можно "переделать" в булево кольцо, определив операцию А + В согласно X (и отбросив операцию A / B). Напр., в случае алгебры множеств роль А + В играет т.н. симметрическая разность множеств А и В (состоящая из всех тех элементов универсума, к-рые принадлежат одному и только одному из множеств А или В). Обратно, всякое булево кольцо (с единицей) можно "переделать" в булеву алгебру. Т.о., теория булевых алгебр и теория булевых колец (с единицей) – лишь разные варианты одной и той же, по существу, теории.

Терминологически понятия булевой алгебры и булева кольца связываются с именем Дж. Буля. Однако оформились эти понятия (не говоря уже о терминах) значительно позже.

В 17 в., когда проблема создания общих методов для решения возможно более широких классов задач была в центре внимания ученых и когда в качестве одного из таких методов (для решения математич. задач) возникла буквенная алгебра. Лейбниц первым предпринял попытку создания аналогичных общих методов (алгоритмов) и для решения задач логики. Однако решить эту задачу ему не удалось. Параллелизм между нек-рыми логич. и алгебраич. операциями подметили также ученики Лейбница, братья Якоб и Иоганн Бернулли (1685). К идеям Лейбница возвращались в дальнейшем Плуке (1763), Ламберт (1764–65), Кастийон (1805) и др. Однако первую А. л. создали (в 1847) только Дж. Буль и А. де Морган. При этом А. л. у Буля носила форму скорее не булевой алгебры, а булева кольца (т.е. была ближе к "языку" УСЕ, чем к "языку" КДО). А. л. в виде булевой алгебры разработали в дальнейшем Джевонс (1864), Пирс (начиная с 1867), Шредер (начиная с 1877), П. С. Порецкий (начиная с 1880). Пирсу и Шредеру принадлежит также разработка начал алгебры отношений. С более общей т. зр., связывающей А. л. с теорией групп, А. л. занимался также в своих первых работах Уайтхед (1898–1903). Строгое построение А. л. как кольца вычетов по модулю 2 (арифметики четного и нечетного, в виде "языка" УСЕ) осуществил (в 1927–1928) И. И. Жегалкин.

Первые работы по А. л. были посвящены задачам: а) выражения логических соотношений между объемами понятий (соответственно, высказываниями) в виде уравнений (равенств), 6) построения алгоритмов решения логич. уравнении и систем уравнений с целью автоматизировать способы извлечения из данных посылок (или систем посылок) содержащейся в них (неявно) информации (того или иного рода). Для обоснования правомерности и практич. целесообразности разработанных ими методов А. л. авторы этих работ нередко предлагали для решения различные логич. задачи. В их числе можно указать, напр., следующую простую задачу, сохранившуюся в истории математич. логики под назв. задачи Венна (1876): известно, что члены (а) правления одной страховой компании суть либо владельцы облигаций (в), либо владельцы акций (с), но не те и другие одновременно. Случайно оказалось, что все владельцы облигаций компании входят в состав ее правления. Что можно сказать на основании этих сведений о соотношении между владельцами акций и владельцами облигаций этой компании? – Естественно, сказать можно, что ни один, вообще, владелец акций не есть, владелец облигаций (в·с=0). Однако, по свидетельству Венна, когда он предложил эту задачу в двух разных классах: обычных студентов-логиков и студентов, изучающих А. л., последние справились с ней значительно лучше.

В наст. время А. л. развивается гл. обр. под влиянием задач, встающих в области ее приложений. Из них самую важную роль играют приложения в теории электрич. схем, включая первоначально, начиная с работ В. И. Шестакова и К. Шеннона (30–40-е гг. 20 в.), теорию релейно-контактных схем, а позднее и схем с иными элементами: электронными лампами, сопротивлениями, полупроводниковыми, ферритовыми элементами и пр. В простейших случаях здесь мы имеем дело еще с одной интерпретацией абстрактной А. л. Она связана, в частности, с тем, что у мн. элементов электрич. схем необходимо различать лишь два состояния, что соответствует паре значений 0 и 1. Так, напр., у контакта имеются два состояния: 1) контакт замкнут, что соответствует 1, 2) контакт разомкнут, что соответствует 0; у 2-полюсной контактной схемы есть два состояния: 1) проводимость между полюсами имеется (в этом случае она считается равной 1), 2) проводимость между ними отсутствует (и считается равной 0). AB при этом соответствует последовательному соединению схем, А / В – параллельному соединению. Уже здесь, в случае произвольной контактной схемы, возникает ряд осложнений по сравнению с положением соответствующих вещей в А. л. Для преодоления нек-рых из связанных с ними трудностей была построена (гл. обр. в работах А. Г. Лунца, 1950–52) алгебра матриц над булевой алгеброй, родственная алгебре отношений. Да и вопросы, касающиеся понятий самой А. л., но встающие под влиянием запросов теории контактных схем (такие, как, напр., вопросы т.н. минимизации и вообще упрощения выражений А. л. путем тождеств. преобразований, а также вопросы различных связанных с этим оценок), приводят к проникновению в А. л. неалгебраич. методов (таких, как табличные, топологические, дескриптивные) и вследствие этого к постепенному выделению из А. л. самостоят. области – теории функций А. л. (или иначе, теории булевых функций).

В случае исследования более сложных схем, чем контактные, приходится часто отказываться от использования лишь обычной двузначной А. л. и рассматривать те или иные ее многозначные обобщения, отличные от булевых алгебр и булевых колец (см. Многозначная логика и Трехзначная логика). В нек-рых работах, тоже в этой связи, намечается выход в область алгебры предикатов (или даже предикатов от предикатов, хотя и принимающих лишь два значения), причем алгебры, более богатой операциями, чем обычная булева алгебра предикатов; напр., Б. А. Трахтенброт рассматривает в алгебраич. аспекте выражения с кванторами по переменным одноместным предикатам и с огранич. кванторами по предметным переменным.

Др. направлением совр. развития А. л. является т.н. алгебраич. логика, связанная с именем Кëрри и др. Она интересна, напр., тем, что выдвигает и частично решает задачу построения алгебр неклассич. логик, т.е. таких вариантов А. л., к-рые соответствуют тем или иным неклассич. исчислениям высказываний, подобно тому, как обычная классич. А. л., т.е. булева алгебра (с импликацией, к-рая в ней, однако, элиминируется, т.к. представима через другие операции), соответствует классич. исчислению высказываний.

Соответствие при этом должно быть таким: любое произвольное тождество U = B должно быть верным в данной А. л., если, и только если, формула U А́ЛГЕБРА ЛО́ГИКИ B доказуема (или обе формулы U → B и B → U доказуемы) в соответствующем ей исчислении высказываний; а формула U должна быть доказуема в данном исчислении высказываний, если, и только если, тождество U = 1 верно в соответствующей ему А. л. Оказывается, что, напр., алгеброй минимальной логики является импликативная структура (или, вернее, теория таких структур), а алгеброй интуиционистской логики является импликативная структура с нулем. В обоих этих случаях свободная импликативная структура и, соответственно, свободная импликативная структура с нулем так же связаны с соответствующими исчислениями высказываний, как свободная булева алгебра с классич. исчислением высказываний.

Наконец, еще нек-рые тенденции возможного дальнейшего развития А. л. как совокупности алгебраич. методов логики намечаются в связи с бурным развитием ряда областей как совр. алгебры, так и математич. логики. Одна из них связана с мощным ростом теоретико-множеств. алгебры как наиболее развитой ветви обшей алгебры, позволяя всякую операцию рассматривать как алгебраич. операцию. Такое рассмотрение, напр., т.н. операций замыкания, в т.ч. функционального замыкания и дедуктивного замыкания, позволяет вопросы функциональной полноты и вопросы дедуктивной полноты и связанные с ними вопросы представимости, непротиворечивости, непополнимости и т.п. рассматривать алгебраически, что дает возможность охватить алгебраич. методами значит. часть совр. математич. логики.

Другая, из этих тенденций связана больше с другой ветвью общей алгебры – с т.н. алгоритмич. алгеброй, к-рая появилась в сер. 20 в. в связи с успехами теории алгоритмов, позволившей уточнить ряд алгоритмич. проблем алгебры, и последовавшим решением (положительным или отрицательным) (Пост, Марков, Новиков, Адян и др.) нек-рых из них. Тенденция эта состоит в объединении алгоритмич. алгебры с самой теорией алгоритмов и попытках алгебраизации последней, т.е. построения алгебраич. теории алгоритмов. Именно, с помощью рассмотрения операций перехода от значений параметров алгоритмич. проблемы к значению ответа на нее алгебраич. операции сведéния произвольной алгоритмич. проблемы (весьма общего вида) к пек-рой проблеме тождества (см. Тождества проблемы), a также нахождения нек-рых критериев разрешимости последней (связанных с алгебраизацией понятия рекурсивной функции) удается дать общий алгебраич. критерий существования алгоритма для данной алгоритмич. проблемы.

Эта постепенная алгебраизация (наряду с охватом и другими чисто математич. методами) все большего числа сторон математич. логики будет, по-видимому, содействовать наилучшему выделению и ее чисто логич. сторон, для того чтобы изучать последние уже иными методами.

Лит.: Яновская С. А., Основания математики и математическая логика, в кн.: Математика в СССР за тридцать лет (1917–1947), М.–Л., 1948; ее же, Математическая логика и основания математики, в кн.: Математика в СССР за сорок лет (1917-1957), т. 1, М., 1959; Порецкий П. С., О способах решения логических равенств и об обратном способе математической логики, Казань, 1884; Жегалкин И. И., Арифметизация символической логики, "Матем. сб.", т. 35, вып. 3–4, М., 1928; Гавpилов Μ. Α., Теория релейно-контактных схем, М.–Л., 1950; Яблонский C.B., О суперпозициях функций алгебры логики, "Матем. сб.", т. 30 (72), вып. 2, М., 1952; Лунц А. Г., Алгебраические методы анализа и синтеза контактных схем, "Изв. АН СССР", Сер. матем., 1952. т. 16, No 5; Тpахтенбpот Б. А., Об операторах, реализуемых в логических сетях, "Докл. АН СССР", 1957, т. 112, No 6; Сборник статей по математической логике и ее приложениям к некоторым вопросам кибернетики, М., 1958; Войшвилло Е. К., Метод упрощения форм выражения функций истинности, "Научн. докл. высшей школы. Философские науки", 1958, No 2; Кузнецов А. В., Алгоритмы как операции в алгебраических системах, "Успехи матем. наук", т. 13, вып. 3, 1958, с. 240–41; Новиков П. С., Элементы математической логики, М., 1959; Гильберт Д. и Аккерман В., Основы теоретической логики, пер. с нем., М., 1947; Биpкгоф Г., Теория структуры, пер. с англ., М., 1952; Тарский А., Введение в логику и методологию дедуктивных наук, пер. с англ., М., 1948; Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; Джевонс В, Ст., Основы науки, пер. с англ., СПБ 1881; Schröder E., Vorlesungen über die Algebra der Logik, Bd l–3, Lpz., 1890–1905; Post E., Introduct, on to a general theory of elementary propositions, "Amer. J. Math.", 1921, v. 43; Boole G., The mathematical analysis of loigic, being an essay towards a calculus of deductive reasoning, Oxf.–N. Y., 1948; его же, An investigation of the laws of thought, on which are founded the mathematical theories of logic and probabilities, N. Y., 1951; Lуndon R. С., Identities in two-valued calculi, "Trans. Amer. Math. Soc.", 1951. v. 71; Curry H. В., Leçons de logique algébrique, P., 1952.

A. Кузнецов. Москва.

Философская Энциклопедия. В 5-х т. — М.: Советская энциклопедия. Под редакцией Ф. В. Константинова. 1960—1970.

АЛГЕБРА ЛОГИКИ

    АЛГЕБРА ЛОГИКИ — одна из осн. частей математической логики, основанная на применении алгебраических методов к логике. Возникнув в сер. 19 в. в трудах Буля и развиваясь затем в работах Джевонса, Шредера, Пирса, Порецкого и др., алгебра логики имела своим предметом классы (как объемы понятий), соотношения между классиками по объему и связанные с этим операции над ними. Позднее, в связи с появлением в 70-х гг. 19 в. множеств теории, поглотившей часть этих задач, предмет алгебры логики значительно изменился. Основным ее предметом стали высказывания (суждения, предложения), рассматриваемые со стороны их логических значений (истина, ложь, бессмыслица и т. п.), и логические операции над ними.

    В основе обычной, т. н. классической алгебры логики лежит абстракция высказывания как величины, имеющей одно (и только одно!) из двух значений; “истина” или “ложь” (короче: И, Л), или могущей принимать оба эти значения (но не одновременно). В первом из этих случаев имеем индивидуальное высказывание (высказывание в узком, наиболее принятом смысле этого слова), во втором—высказывание-функцию. Примеры высказываний: “22= 4”, “OSÛ”, “Сократ—человек”, “0°1”, “2•2=!5”, <сс2^”, “г—человек”, “Если х=у, то у=0”, “Если χ=ΐ, то х^”, “х равняется у или χ не равняется у*. Первые три высказывания имеют значение И (т. е. истинны), 4-е и 5-е—значение Л (т. е. ложны), 6-е, 7-е, 8-е— высказывания-функции (если, напр., значениями буквенных переменных х к у могут быть целые числа, а переменной г—живые существа), 9-е и 10-е имеют значение И (при всех возможных значениях переменных х и у). Последние три из этих высказываний являются сложными, в отличие от предшествующих им простых. Абстракция в алгебре логики идет дальше. Все истинные высказывания отождествляются между собой, т. к. истинное высказывание не отличается от другого истинного высказывания по значению (от других сторон высказываний в алгебре логики отвлекаются). Ложные высказывания тоже отождествляются. При рассмотрении же высказываний-функций в алгебре логики обычно отвлекаются от рассмотрения зависимости их от иных переменных, кроме таких, значениями которых тоже являются высказывания, вводя для их рассмотрения буквенные переменные, которые называют переменными высказываниями. Таковыми являются буквы А, В, С, ..., Ai, Ai, Ai, ... и т. п. (при этом выбор букв—вопрос не существа, а соглашения) при условии, что они играют роль переменных, значениями которых могут быть всевозможные индивидуальные высказывания, т. е., в силу упомянутых абстракций, “константы” И и Л.

    Кроме простых высказываний, обозначаемых отдельными буквами А, В... или И, Л, рассматриваются также сложные высказывания — результат соединения высказываний связками или отрицания их (соответствующего частице “не”). Сложные высказывания рассматривают как функции от входящих в них буквенных переменных А, В, С и τ. д. Так появляется понятие функции алгебры логики — функции от аргументов, являющихся переменными высказываниями, т. е. принимающих значения И, Л, которая (функция) может принимать тоже лишь эти значения.

    Вводятся алгебраич. операции над высказываниями: конъюнкция А•В (читается “А и В”, другие обозначения: AB, А&.В, АлВ; другие названия: логическое умножение, булево умножение), дизъюнкция AvB (читается <А или В”; другое обозначение: А+В; другие названия: логическое сложение, булево сложение), импликация А-В (читается: “Если А, то J?” или “Л влечет В”, или “А имплицирует Во, или “Из А следует В”; другое обозначение: ЛэД; другое название: логическое следование), эквиваленция А—В (читается: “А эквивалентно В” или “А равнозначно В*, или *А, если и только если Д”; другие обозначения: А=В, А<->В, А=В; другие названия: эквивалентность, равнозначность, равносильность), отрицание À (читается: “не А”, или ιΑ ложно”, или “неверно, что А”, или “отрицание А”; другие обозначения: -А, АЛГЕБРА ЛОГИКИА, А; другое название: инверсия), а также иногда и другие операции.

    Одной из важных сторон формализации, принимаемой в алгебре логики, является то, что знаками этих операций (т. е. по смыслу, соответствующими им связками) можно соединять любые высказывания, без ограничения, в том числе и те, которые сами являются сложными.

    При этом удается точно и строго описать класс всех рассматриваемых выражений алгебры логики. В данном случае он состоит из констант И и Л, переменных А, В... и всех тех выражений, которые получаются из них путем конечного числа соединений знаками “ ”, “v”, “->” и “АЛГЕБРА ЛОГИКИ” и отрицаний.

    Это связано с требованием, чтобы операции задавались таблично как функции и значение сложного высказывания зависело только от значений составляющих его простых высказываний. Основная суть алгебры логики как системы методов состоит в использовании преобразований высказываний на основе алгебраических законов, которые имеют место для операций над высказываниями. Эти законы чаще всего имеют вид тождеств, т. е. равенств, верных при всех значениях переменных. Важную роль играют тождества: Ι. АВ=ВА, ΑνΒ"ΒνΑ (законы коммутативности), П. (АВ)ОА(ВС), {AvB)vC^A•v(BvQ (законы ассоциативности); III. A(AvB)asA, AvAB = А (законы поглощения); P/. A(BvQ " АВ^АС (закон дистрибутивности); V. А-^Л (закон противоречия); VI. Αν-Α=Ά (закон исключенного третьего). Эти тождества, устанавливаемые, напр., с помощью таблиц, позволяют получать другие тождества. Тождеств I—V! достаточно для того, чтобы из них по методу тождественных преобразований можно было вывести всякое (верное, конечно) тождество, левая и правая части которого—выражения алгебры логики, состоящие из переменных А, В, .., констант И, Л и знаков “•”, “ν” “-τ” (не обязательно включая все из них). Добавление же тождеств VII А->В=-А/В, AАЛГЕБРА ЛОГИКИB=ABv-iA-J! дает возможность выводить и любые тождества, содержащие также знаки “-””, “АЛГЕБРА ЛОГИКИ”. Тождества V, VI, VII показывают, что константы И и Л, импликацию и эквиваленвию, рассматривая их как функции, можно выразить через конъюнкцию, дизъюнкцию и отрицание. Имеет место теорема, гласящая, что всякая функция алгебры логики может быть представлена через эти три операции, т. е. записана в виде выражения, содержащего лишь знаки этих операций и буквенные переменные. Именно, любую функцию Φ(Αι, Αι, ... , Ал) можно записать как дизъюнкцию всех выражений вида

    Φ(οι, иг,.... α.)•(ΑίАЛГЕБРА ЛОГИКИαι)(ΑιАЛГЕБРА ЛОГИКИαι)...(Α.АЛГЕБРА ЛОГИКИα^, где βι, ai,.., β,— набор из значений И, Л. Заменяя в этой дизъюнкции выражения ΑιАЛГЕБРА ЛОГИКИΆ на Ai, a Аг-Л—т -Ai, a также стирая “коэффициенты” Φ(ΰι, αϊ, ..., а.), равные И (по закону К•А'°А) и отбрасывая члены с “коэффициентами”, равными Л (по законам (Л•Д•°Л, ЛуЛ — А), мы и получим (если функция не есть константа) то выражение, о котором говорится в теореме.

    Дизъюнктивной нормальной формой (днф) называется выражение, которое есть буква И или Л или имеет swAivAiv... vA„ где каждый член Αι является либо буквенной переменной, либо ее отрицанием, либо конъюнкцией таковых, причем s не обязательно отлично от 1, т. е. знаков “ν” может и не быть. Днф называется совершенной, если она есть И или Л или в каждом члене содержит ровно по одному разу все имеющиеся в ней буквы (переменные) и не имеет одинаковых членов. Всякое выражение алгебры логики можно привести к днф. А всякую днф можно привести к совершенной днф, “домножая” члены на недостающие буквы (по закону A-ABvA-Jf) и ликвидируя повторения букв в членах (по законам АА^А, А-*4•°Л, Л•Л""Л, ΠνΑ^Α) и повторения членов (по закону AvA-A).

    Приведение к совершенной днф позволяет по любым двум данным выражениям А и В решить вопрос о том, одну ли и ту же функцию они выражают, т. е. верно ли тождество А^В.

    Важную роль играет т. н. сокращенная днф. Последнюю можно определить как такую днф, в к-рой 1) нет повторений букв ни • одном члене, 2) нет таких пар членов Αι и А/, что всякий множитель из Αι имеется и в Л/, и 3) для всяких двух таких членов, из к-рых один содержит множителем некоторую букву, а другой— отрицание той же буквы (при условии, чтодругой буквы, для которой это имеет место, в данной паре членов нет), имеется (в этой же днф) член, равный конъюнкции остальных множителей этих двух членов.

    Кроме днф, употребляются также конъюнктивные нормальные формы (кнф). Это такие выражения, к-рые можно получить из днф путем замены в них знаков “ν” на “•”, а “•” на “ν”.

    Преобразованием двойственности называется такое преобразование выражения алгебры логики, при котором в этом выражении знаки всех операций заменяются на знаки двойственных им операций, ” константы: И на Л, Л на И; причем операция (или функция) Φ называется двойственной для операции Ψ, если таблица, задающая Ф, получается из таблицы, задающей Ψ, путем замены в ней всюду И на Л, а Л на И (имеется в виду одновременная замена и значений функции, и значений ее аргументов). Если Ф двой

    ственная Ψ, a Ψ двойственная X, то Ф=Х. Напр., конъюнкция и дизъюнкция двойственны между собой, отрицание двойственно самому себе, константа И (как функция) двойственна константе Л. Функция Φ(^ι, А-г,..., Л„) двойственна функции ЧЧ,Аь Ai,..., А.), если, и только если, верно тождество

    -,Ф(Д„ Аг...., 4,)”Ψ (-ι4, -.At,.... -,Α.).

    Совершенную кнф и сокращенную кнф можно определить как такие кнф, что двойственные им выражения есть соответственно совершенная днф и сокращенная днф. Совершенные и сокращенные днф и кнф можно использовать для решения задачи обзора всех гипотез и всех следствий данного выражения алгебры логики Причем под гипотезой выражения А алгебры логики естественно понимать такое выражение В, что В->А тождественно истинно, а под следствием выражения Л—такое выражение В, что А—>В тождественно истинно.

    Еще один, часто употребляемый в алгебре логики шаг абстракции, состоит в отождествлении И с числом 1, а Л — с числом 0. Вводится операция А+В, задаваемая таблицей: 0+0=0, 0+1=1, 1+0=1,1+1=0. Она называется сложением (точнее сложением по модулю 2; другое название: разделительная дизъюнкция; читается: “А плюс В”, или А не эквивалентно В”, или “Либо А, либо Д”). Всякую функцию алгебры логики можно представить через умножение (т. е. конъюнкцию), сложение и константу 1 (теорема Жсгалкина). В частности, верны следующие тождества; VIII. AvB=AB+A+B, -i/l=4+l DC A-^BaAB•^•A+1, ΑАЛГЕБРА ЛОГИКИΒ"Α+Β+1.

    Обратные представления имеют вид

    X. A+B^A-^v-^AB, l=/lv-^.

    Тождества VIII позволяют “переводить” выражения “языка” конъюнкции, дизъюнкции и отрицания (КДО) на “язык” умножения, сложения и единицы (УСЕ), а тождества X—осуществлять обратный “перевод”.

    Тождественные преобразования можно производить и на “языке” УСЕ. В основе их лежат следующие законы: XI. АВ=ВА. А+В^В^-А (законы коммутативности); XII. (АВ)С=А<.ВС), (Л+^)+С^+(Д+0 (ассоциативности); XIII. А(В+С)"АВ+АС (закон дистрибутивности); XIV. АА”А, А+(В+В)=А

    XV. АЛ=А.

    Этих тождеств достаточно для того, чтобы из них можно было вывести любое (верное) тождество, обе части которого суть выражения “языка” УСЕ. А добавив к ним тождества VIII, мы сможем выводить и все тождества “языка” КДО.

    Выражение “языка” УСЕ называется приведенным полиномом (п. п.), если оно есть 1+1 (т. е. нуль) или имеет вид А^А]+ ... +А„ где каждый член Αι есть либо 1, либо буквенная переменная, либо произведение последних, причем ни в одном члене нет никаких повторений букв, никакие два члена не одинаковы (в том же смысле, что и выше), a s не обязательно больше 1 (т. е. знаков “+” может не быть). Всякое выражение алгебры логики можно привести к п. п. (теорема Жегалкина).

    Кроме “языков” КДО и УСЕ существуют и другие “языки”, обладающие тем свойством, что через операции (и константы) этих “языков” можно представить всякую функцию алгебры логики. Такие системы называются (функционально) полными. Примеры полных систем: а) конъюнкция и отрицание, б) дизъюнкция и отрицание, в) импликация и отрицание, г) импликация и 0, д) умножение, эквиваленция и 0, е) штрих Шеффера А[В, ж) медиана (Л, В, С), (определение: (А, В, C)=ABvACvBC, отрицание и 1, и) медиана, эквиваленция и сложение.

    Иногда совершают еще один важный дальнейший шаг абстракции. Отвлекаются от табличного задания операций и от того, что значениями буквенных переменных являются высказывания. Вместо этого допускаются различные интерпретации рассматриваемого “языка”, состоящие из той или иной совокупности объектов (служащих значениями буквенных переменных) и системы операций над объектами этого множества, удовлетворяющих тождествам из полной системы тождеств этого “языка”.

    “Язык” КДО в результате такого шага абстракции превращается в “язык” т. н. булевой алгебры, “язык” УСЕ—в “язык” т. н. булева кольца (с единицей), .“язык” конъюнкции и дизъюнкции — в “язык” т. н. дистрибутивной структуры.

    Важным примером булевой алгебры является алгебра классов, в которой роль элементов играют подмножества (классы) некоторого фиксированного множества (т. н. универсума) V, роль 0 играет пустое множество 0, роль 1—само Ü, роль AS, AvB и -ιΑ— теоретико-множеств. операции пересечения, объединения и дополнения соответственно. Связь между алгеброй классов, алгеброй предикатов и алгеброй высказываний, этими тремя важнейшими интерпретациями абстрактной алгебры логики как “языка” булевой алгебры, состоит в следующем: первая переходит во вторую путем замены множеств (классов) их т. н. характеристическими предикатами (т. е. множества Л—предикатом хеА, гласящим: “х принадлежит множеству А*), если при этом соответствующим образом преобразуются также операции и константы 0 и I, а вторая переходит в третью при подстановке во все предикаты на место их аргументов некоторого фиксированного их значения. Вернее, при таком переходе от алгебры классов к алгебре предикатов получается алгебра одноместных предикатов. Другим важным случаем является алгебра двуместных предикатов, называемых чаще отношениями. С ней тесно связана алгебра отношений, отличающаяся от нее только тем, что в последней, кроме трех операций булевой алгебры, имеются еще две.

    Всякую булеву алгебру можно “переделать” в булево кольцо, определив операцию А+В согласно закону Χ (и отбросив операцию Ανΰ). Напр., в случае алгебры множеств роль А+В играет т. н. симметрическая разность множеств А и В (состоящая из всех тех элементов универсума, которые принадлежат одному и только одному из множеств А или ΰ). Обратно, всякое булево кольцо (с единицей) можно “переделать” в булеву алгебру. Понятия булевой алгебры и булева кольца связываются с именем Дж. Буля. Однако оформились эти понятия (не говоря уже о терминах) значительно позже, Первые работы по алгебре логики были посвящены задачам: а) выражения логических соотношений между объемами понятий (соответственно высказываниями) в виде уравнений (равенств), б) построения алгоритмов решения логических уравнений и систем уравнений с целью автоматизировать способы извлечения из данных посылок содержащейся в них (неявно) информации (того или иного рода).

    В настоящее время алгебра логики развивается гл. о. под влиянием задач, встающих в области ее приложений. Она находит широкое применение в технике (особенно при решении задач, связанных с построением автоматов) и, наоборот, развивается сама под влиянием запросов техники (задач автоматизации программирования, уменьшения числа элементов в устройствах релейного действия и др.). Важную роль играют приложения в теории электрических схем, включая первоначально, начиная с работ В. И. Шестакова и К. Шеннона (30—40-е гг. 20 в.), теорию релейно-контакгных схем. Вопросы, касающиеся понятий самой алгебры логики, приводят к проникновению в алгебру логики неалгебраических методов (таких, как табличные, топологические, дескриптивные) и вследствие этого к постепенному выделению из алгебры логики самостоятельной области—теории функций алгебры логики (или иначе, теории булевых функций).

    В случае более сложных схем, чем контактные, приходится часто отказываться от использования лишь обычной алгебры логики и рассматривать те или иные ее многозначные обобщения, отличные от булевых алгебр и булевых колец (см. Многозначные логики). Другим направлением современного развития алгебры логики является алгебраическая логика. Она интересна тем, что выдвигает и частично решает задачу построения алгебр неклассических логик, т. е. таких вариантов алгебры логики, которые соответствуют неклассическим исчислениям высказываний.

    Некоторые тенденции возможного дальнейшего развития алгебры логики как совокупности алгебраических методов логики намечаются в связи с бурным развитием ряда областей как современной алгебры, так и математической логики. Одна из них связана с мощным ростом теоретико-множественной алгебры, позволяя всякую операцию рассматривать как алгебраическую операцию. Такое рассмотрение дает возможность охватить алгебраическими методами значительную часть современной математической логики (см. Логика символическая).

    Другая—связана с успехами теории алгоритмов, позволившей уточнить ряд алгоритмических проблем алгебры, и последовавшим решением некоторых из них. Тенденция эта состоит в объединении алгоритмической алгебры с самой теорией алгоритмов и попытках алгебраизации последней, т. е. построения алгебраической теории алгоритмов.

    Эта постепенная алгебраизация все большего числа сторон математической логики будет, по-видимому, содействовать наилучшему выделению и ее чисто логических сторон, для того чтобы изучать последние уже иными методами.

    Α. ΰ. Кузнецов

    Сокращенный вариант статьи: Алгебра логики.— В кн.: Философская энциклопедия. Т. 1. M., I960.

    Как и предвидел А. Кузнецов, все большее прикладное значение приобретает теория булевых функций как самостоятельная область, выделившаяся из алгебры логики. В результате пришли к понятию функциональной системы (Ря, С), где Ря есть множество всех функций и-значной логики (или множество всех функций счетаозначной логики Р”) с заданной на нем операцией суперпозиции С. Р, обычно рассматривается как обобщение множества всех булевых функций Рг. Известна содержательная трактовка понятия функциональной системы ((Р„ С) выступает ее частным случаем), в основе которой лежит рассмотрение таких пар (Ρ, Ω), в которых Р есть множество отображений, реализуемых управляющими системами из некоторого класса, a Ω состоит из операции, используемой при построении новых управляющих систем из заданных. В свою очередь (Рг, С) есть эквивалент алгебры логики. Таким образом, от алгебры формул, изучаемой в алгебре логики, перешли к алгебре функций. И хотя именно алгебра логики, т. е. классическая логика высказываний, лежит в основе проектирования микросхем для современной цифровой электронной техники, в том числе и для компьютеров, подобные работы ведутся и на основе многозначных логик. В частности, для функционально полных (и некоторых других) многозначных систем был построен аналог совершенной днф, Еще более важное предвидение А. Кузнецова связано с выделением алгебраической логики в одно из направлений современной алгебры логики. В первую очередь имеется в виду построение алгебр, соответствующих неклассическим логикам в том смысле, в каком булева алгебра соответствует классической логике высказываний (Rasiowa, 1974). Здесь существенным является также вопрос о построении алгебраической семантики, под которой понимается класс всех моделей некоторой алгебры, соответствующей логике L, поскольку посредством алгебраической семантики решаются такие металогические проблемы, как полнота L (относительно общезначимости в классе всех моделей), разрешимость L и др. В итоге пришли к общему вопросу о том, какая логика алгебраически представима, т. е. имеет алгебраическую семантику, а какая нет. Ответ на этот вопрос дан в работе В. Блока и Д. Пигоцци (Blök, Pigozzi, 1989). Существенно, что современное развитие алгебраической логики представляет собой систематическое применение методов и, главное, аппарата универсальной алгебры к символической логике. Именно на это как на тенденцию возможного дальнейшего развития алгебры логики указывал А. Кузнецов, говоря о возможности “охватить алгебраическими методами значительную часть современной математической логики”. Сегодня речь уже идет об алгебраическом охвате всей символической логики, и результаты здесь весьма значительны. К примеру, если Alg(L) обозначает класс алгебр, который соотносится с некоторой логикой L (если L есть классич. логика высказываний, то Alg(L) есть класс булевых алгебр), можно формулировать теоремы, утверждающие, что L имеет определенное логическое свойство тогда и только тогда (т. т. т.), когда Alg(L) имеет определенное алгебраическое свойство. Это позволяет дать алгебраическую характеризацию таких логических свойств, как полнота, наличие теоремы дедукции, компактность, разрешимость, интерполяционность Крейга, истинность формул в модели и т. д. Так, первые два свойства принимают следующий вид; L допускает строго полную гильбертовскую аксиоматизацию (Г^-А т. т. т., когда Г•=Л) т.т.т., когда Alg(L) есть финитно аксиоматизируемое квази-многообразис; L допускает теорему дедукции (см. Дедукции теорема) τ.τ.τ., когда Alg(L) имеет эквационально определимые главные конгруэнции.

    Вообще, алгебраическая логика является хорошим инструментом не только для выяснения взаимоотношения между различными логическими системами, но и для уточнения статуса логики.

    Лит.: Жегалкин И. И. Арифметизация символической логики.— “Матем. сб.”, т. 35. Вып. 3—4. M., 1928; Яновская С. А. Основания математики и математическая логика.—В кн.: Математика в СССР за тридцать лет (1917—1947). M.—Л., 1948; Она же. Математическая логика и основания математики.—В кн.: Математика в СССР за сорок лет (1917—1957), т. l. M., 1959; Сб. статей по математической логике и ее приложениям к некоторым вопросам кибернетики. М, 1958; Войшвимо ?. К. Метод упрощения форм выражения функций истинности,—“Философские науки”, 1958, № 2; Кузнецов А. В. Алгоритмы как операции в алгебраических системах.— “Успехи математических наук”, 1958, т. 13, в. 3, Новиков П. С. Элементы математической логики. М., 1973; Биркгоф Г. Теория решеток. М., 1952; Владимиров Д. А. Булевы алгебры. 1969; Гчндикин С. Г. Алгебра логики, в задачах. М., 1972; Кудрявцев В. Б. О функциональных системах. М., 1981; Яблонский С. В., Гавршов Г. П., Кудрявцев В. Б. Функции алгебры логики и классы Поста. М., 1966; Фридлендер Б. И; Ревякин А. М. Булева алгебра и ее применение в задачах электроники: учебное пособие. М., 1993; Algebraic logic and the methodology of applying it.—CSLI Publications, 1995; Anderka H., Nemeti I., Sain I. Algebraic Logic.— Handbook of philosophical logic (2 éd.), forthcoming; Blök W. J., Pigozü D. Algebraizable logics (monograph).—Memoirs of the American Mathematical Society, 1989, ¹ 396; fbnt J. M., Jansana R. A general algebraic semantics for sentential logics. В., 1996; Handbook of Boolean algebras, Ed. J. D. Monk with the coop. R. Bennet, v. I—III. Amst., 1989; Nemeti I., Anderka H. General algebraic logic: a perspective on “What is logic”.— What is logical system? Oxf-, 1994; N. Y., 1995; Rasuma H. An algebraic approach to non-classical logics. Warsz., 1974.

    А. С. Карпенко

Новая философская энциклопедия: В 4 тт. М.: Мысль. Под редакцией В. С. Стёпина. 2001.