ШРЁДИНГЕРА УРАВНЕНИЕ НЕЛИНЕЙНОЕ

ШРЁДИНГЕРА УРАВНЕНИЕ НЕЛИНЕЙНОЕ

- нелинейное дифференциальное ур-ние в частных производных

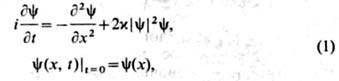
где 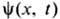-комплекснозначная ф-ция (заряж. скалярное поле). Вещественный параметр 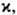входящий в ур-ние, играет роль константы связи. Своё название Ш. у. н. получило из-за формального сходства с Шрёдингера уравнением для свободной одномерной частицы, в к-рое ур-ние (1) переходит в линейном пределе 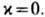В физ. приложениях ур-ние (1) возникает при исследовании широкого класса нелинейных явлений, в частности в физике плазмы, в нелинейной оптике и др.

Ш. у. н. может быть проинтегрировано с помощью обратной задачи рассеяния метода. В основе данного метода лежит представление ур-ния (1) в виде условия совместности переопределённой системы ур-ний (вспомогат. линейной задачи):

Здесь F -двухкомпонентный вектор-столбец, зависящий от х, t и нек-рого произвольного комплексного числа получившего назв. "спектральный параметр", - матрицы

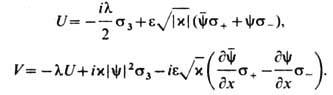
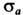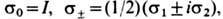
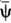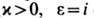Здесь и в дальнейшем - Паули матрицы( а = 0, 1, 2, 3), -ф-ция, комплексно-сопряжённая ф-ции при при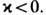

Выполнение условия совместности для вспомогательной линейной задачи

эквивалентно выполнению ур-ния (1). Запись ур-ния (1) в виде (1') принято называть представлением нулевой кривизны.

Альтернативно метод обратной задачи рассеяния может быть сформулирован на основе представления Лакса.

Центр, объектом в методе обратной задачи рассеяния является матрица монодромии 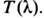Для определения последней необходимо ввести матрицу перехода удовлетворяющую ур-нию

Конкретное выражение матрицы монодромии через матрицу перехода зависит от вида граничных условий, накладываемых на ф-цию Предположим, что решение Ш. у. н. ищется в классе быстроубывающих ф-ций с нач. условием

Тогда

Замечательным свойством матрицы монодромии является особенно простая зависимость её матричных элементов от времени:

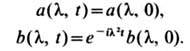
Ф-ци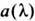и и 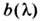принято называть коэф. перехода. В теории рассеяния величины 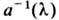и 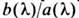играют роль коэф. прохождения и отражения. Решение 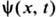ур-ния (1) однозначно восстанавливается по данным рассеяния и сводится к исследованию аналитич. свойств коэф. перехода. Конкретно это может быть сделано с помощью методов задачи Римана о факторизации матрицы или с помощью интегральных ур-ний Гельфанда-Левитана - Марченко. В частном случае безотражательного потенциала 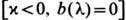решение находится явно и называется N -солитонным [где N -число нулей коэф.].

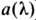С помощью метода обратной задачи рассеяния также находится решение задачи Коши для граничных условий вида (условия конечной плотности). В этом случае обычно в правую часть ур-ния (1) добавляют линейное по y слагаемое (соответственно в представлении нулевой кривизны матрица V заменяется на ).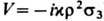

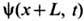
В случае периодич. граничных условий 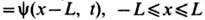решение Ш. у. н. сводится к исследованию вспомогат. линейной задачи на римановой поверхности ф-ции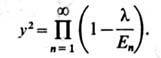

Здесь 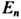-границы разрешённых и запрещённых зон в спектре оператора 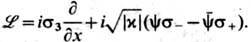В случае, когда число зон конечно, решение 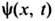ур-ния (1) допускает явное выражение через 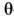-функции Римана и наз. конечнозонным. При конечнозонные решения Ш. у. н. переходят в N -солитонные.

Ш. у. н. можно рассматривать как гамильтоново ур-ние движения 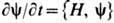с гамильтонианом

и скобкой Пуассона . Координатами в фазовом пространстве являются ф-ции 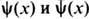с определ. граничными условиями.

В рамках гамильтонова подхода к Ш. у. н. широкое распространение получил метод r-матрицы, первоначально возникший в теории квантового метода обратной задачи. В основе данного метода лежит возможность представить скобки Пуассона матричных элементов матрицы 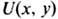в виде

где r -матрица равна

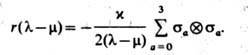
Можно показать, что такая запись скобок Пуассона заменяет представление нулевой кривизны.

Скобки Пуассона матричных элементов матрицы моно-дромии также записываются с помощью r-матрицы:

С точки зрения гамильтонова подхода переход к данным рассеяния является канонич. преобразованием к переменным действие - угол.

Гамильтонова модель Ш. у. н. является вполне интегрируемой и обладает бесконечным набором интегралов движения производящей ф-цией для к-рых является след матрицы монодромии 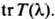Все интегралы движения записываются в виде локальных функционалов от 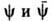и их производных, напр.:

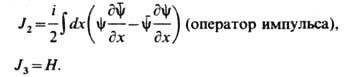
Ур-ния видапринято называть высшими

Ш. у. н.

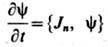
Векторное Ш. у. н. описывает движение заряж. скалярного поля 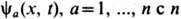цветами:

где под 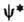подразумевается вектор-столбец, эрмитово сопряжённый к вектор-строке 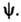Векторное Ш. у. н., как и скалярное, представимо в виде условия нулевой кривизны. Матрицы U и V в этом случае имеют размерность 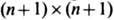и в блочной записи являются прямым обобщением матриц U к У скалярного ур-ния. Гамильтониан модели и скобки Пуассона даются ф-лами

Иногда в литературе под термином "Ш. у. н." подразумевают систему ур-ний

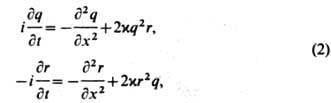
причём ф-ции q и r, вообще говоря, не являются комплексно сопряжёнными. Большинство результатов для ур-ния (1) справедливо и для системы (2), однако в последнем случае для разрешимости обратной задачи рассеяния требуется накладывать ряд дополнит, условий на данные рассеяния. Помимо стандартных методов для системы (2) существует метод построения решения с помощью преобразования Беклунда - Шлезингера. А именно, если 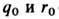- решения (2), то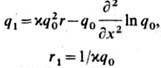

также - решения (2). Указанное преобразование является простым способом построения солитонных решений ур-ния (1). А именно, в качестве затравочного решения системы (2) выбирается r₀ = 0, q₀- общее решение свободного ур-ния. После N -кратного применения преобразования Беклунда - Шлезингера к q₀ и r₀ и наложения условия получаем N -солитонное решение ур-ния (1). Ряд разностных ур-ний, к-рые в непрерывном пределе переходят в Ш. у. н., обычно называют решёточными Ш. у. н. К таким ур-ниям относится, напр., ур-ние Абловитца-Ладика: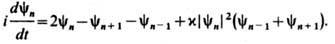

Это ур-ние является гамильтоновым и вполне интегрируемым. Переход от непрерывной ф-ции 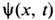к дискретной переменной 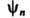часто используется при квантовании Ш. у. н.

Квантовое Ш. у. н.

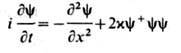
описывает квантовую одномерную систему многих частиц с парным взаимодействием, к-рое задаётся потенциалом Здесь являются соответственно операторами рождения и уничтожения, действующими в Фока пространствеОдновременные перестановочные соотношения задаются ф-лой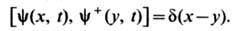

Гамильтониан модели

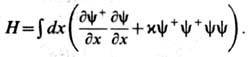
Квантовое Ш. у. н. допускает представление нулевой кривизны, аналогичное представлению для классического Ш. у. н. Перестановочные соотношения между матричными элементами матрицы монодромии, к-рая определяется так же, как и в классич. случае, задаются с помощью квантовой R -матрицы:

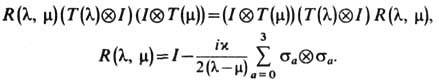
Как и классическое, квантовое Ш. у. н. является вполне интегрируемым и обладает бесконечным набором интегралов движения. Многочастичная матрица рассеяния сводится к произведению двучастичных матриц рассеяния.

Квантовое Ш. у. н. решается с помощью анзаца Бете. Конкретная формулировка анзаца Бете зависит от вида граничных условий, налагаемых на операторы 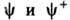В случае периодич. задачи на отрезке 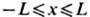собственные ф-ции гамильтониана H ищутся в виде

Ф-ция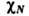 при этом определяется из условия и параметризуется набором параметров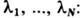

Здесь сумма берётся по перестановкам переменных l₁, ..., 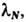к-рые в свою очередь должны удовлетворять системе ур-ний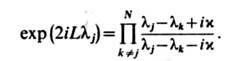

Собственные значения гамильтониана

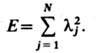
В рамках квантового метода обратной задачи собственные ф-ции гамильтониана Я строятся с помощью матричных элементов матрицы монодромии и выглядят особенно просто:

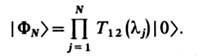
В случае притяжения (x<0) в модели возможны связанные состояния, к-рые иногда называют квантовыми солитонами.

Корреляц. ф-ции квантового Ш. у. н. могут быть выражены в терминах детерминантов Фредгольма. В пределе 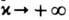(непроницаемый бозе-газ) корреляц. ф-ции операторов 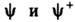выражаются через решения классич. системы (2).

Лит.: Захаров В. E., Шабат А. Б., Точная теория двумерной самофокусировки и одномерной автомодуляции волн в нелинейных средах, "ЖЭТФ", 1971, т. 61, в. 1, с. 118; Теория солитонов. Метод обратной задачи, M., 1980; Тахтаджян Л. А., Фаддеев Л. Д., Гамильтонов подход в теории солитонов, M., 1986; НьюэллА., Солитоны в математике и физике, пер. с англ., M., 1989; Ko-repin V. E., Bogoliubov N. M., Izergin A. G., Quantum inverse scattering method and correlation functions, Cambr., 1993.

H. А. Славное.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.