- НЕЛИНЕЙНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- НЕЛИНЕЙНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
-
- ур-ния, не обладающие свойством линейности; применяются в физике как матем. модели нелинейных явлений в разл. сплошных средах. Н. у. м. ф.- важная часть матем. аппарата, используемого в фундам. физ. теориях: теории тяготения и квантовой теории поля.
Строго говоря, все сплошные среды описываются нелинейными ур-ниями. Выбор для описания среды линейных или нелинейных ур-ний зависит от роли, к-рую играют нелинейные эффекты, и определяется конкретной физ. ситуацией. Напр., при описании распространения лазерных импульсов необходимо учитывать зависимость показателя преломления среды от интенсивности эл.-магн. поля. Возникающие при этом Н. у. м. ф. являются основой матем. аппарата нелинейной оптики.
Линейные ур-ния, используемые в физике, являются результатом линеаризации более точных Н. у. м. ф. на фоне их простейших (фоновых) решений. Исторически первым примером Н. у. м. ф. были найденные в 18 в. Эйлера уравнения для идеальной жидкости:
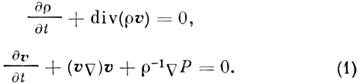
Здесь r, Р,u - плотность, давление и скорость жидкости. Для баротропной жидкости, когда Р= Р(r), ур-ния Эйлера можно линеаризовать на фоне тривиального решения r = r0, u0 =0 в предположении потенциальности поля скоростей: u =
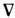 j. Полагая r = r0 + dr, dr << r0, получаем из (1) волновое уравнение для звуковых волн. Однако при рассмотрении вихревых движений жидкости, когда её можно считать несжимаемой, r = r0, div u = 0, ур-ния Эйлера (1) становятся существенно нелинейными. Их линеаризация на фоне решения u0.= 0 приводит к тривиальному ур-нию дu/дt =0.
j. Полагая r = r0 + dr, dr << r0, получаем из (1) волновое уравнение для звуковых волн. Однако при рассмотрении вихревых движений жидкости, когда её можно считать несжимаемой, r = r0, div u = 0, ур-ния Эйлера (1) становятся существенно нелинейными. Их линеаризация на фоне решения u0.= 0 приводит к тривиальному ур-нию дu/дt =0.Т. о., линеаризация Н. у. м. ф. не всегда ведёт к содержат. результату. Может оказаться, что линеаризация имеет смысл, но линейные ур-ния сохраняют применимость лишь конечное время. Эта ситуация типична, если фоновое решение неустойчиво, но может иметь место и при устойчивом фоновом решении. Так, одномерные ур-ния Эйлера
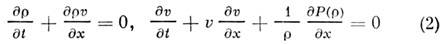
при произвольном нач. условии r
 r0, u
r0, u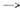 .0 при х
.0 при х . описывают образование ударных волн. При этом за достаточно большое время теряют применимость не только линейное приближение, но и сами ур-ния (2), решения к-рых при t
. описывают образование ударных волн. При этом за достаточно большое время теряют применимость не только линейное приближение, но и сами ур-ния (2), решения к-рых при t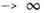 становятся неоднозначными.
становятся неоднозначными.Даже если линеаризация Н. у. м. ф. возможна, с точки зрения физики исключительно важны "существенно нелинейные" решения, качественно отличающиеся от решений линейных ур-ний. Такими могут быть стационарные решения солитонного типа, локализованные в одном или неск. измерениях (см. Солитон), или решения типа волновых коллапсов, описывающие самопроизвольную концентрацию энергии в небольших областях пространства (см. также Самофокусировка света). Существенно нелинейными являются и стационарные решения ур-ний гидродинамики. Весьма важен вопрос об устойчивости существенно нелинейных решений, в т. ч. гидродинамич. течений и солитонов, к-рый решается либо при помощи линеаризации Н. у. на фоне изучаемых решений, либо при помощи вариац. оценок.
Решения Н. у. м. ф. во мн. случаях обнаруживают тенденцию к стохастизации. В этом случае они требуют статистич. описания, что составляет предмет теории турбулентности. Турбулентность часто развивается как результат неустойчивости фонового состояния. Если уровень нелинейности решения остаётся малым, то говорят о слабой турбулентности, в противном случае - о сильной турбулентности. Сильная турбулентность может сопровождаться волновыми коллапсами, целиком или частично состоять из взаимодействующих солитонов.
Нелинейные уравнения в физике. Н. у. м. ф., встречающиеся в физике, отличаются большим разнообразием. Их значит. часть представляет собой обобщения гидродинамич. ур-ний Эйлера, напр. Навье - Стокса уравнения для описания движений вязкой несжимаемой жидкости. Описываемая ими гидродинамич. турбулентность является предельно сильной.
В метеорологии были выведены ур-ния Буссинеска, описывающие движения несжимаемой жидкости в поле тяжести и сил Кориолиса и используемые в океанологии и физике атмосферы. Ур-ния магнитной гидродинамики описывают движение проводящей жидкости в магн. поле и применяются в астрофизике и физике плазмы.
Классич. примером Н. у. м. ф. являются уравнения теории упругости. Развитие микроскопической теории кристаллов дополнило их уравнениями равновесия и динамики дислокаций, также существенно нелинейными.
Многие Н. у. м. ф. возникли в физике в связи с развитием теории конденсиров. сред, они описывают мак-роскопич. проявления квантовомеханич. эффектов; неизвестной ф-цией в них является плотность параметра порядка (см. Фазовый переход). Если параметр порядка скалярный, это двухжидкостные ур-ния гидродинамики сверхтекучего гелия (см. Сверхтекучесть), ур-ния Гинзбурга - Ландау и их обобщения, описывающие магнетостатику и электродинамику сверхпроводников (см. Сверхпроводимость). Если параметр порядка векторный или тензорный, это ур-ния Ландау - Лифшица, описывающие ферромагнетики и антиферромагнетики, ур-ния обобщённой гидродинамики сверхтекучего гелия, макроскопич. модели жидких кристаллов. Для всех этих ур-ний наиб. интерес представляют их существенно нелинейные решения, часто описывающие локализованные (хотя бы частично) объекты: вихри в жидком гелии и в сверхпроводниках, доменные стенки в ферромагнетиках и антиферромагнетиках, дисклинации в жидких кристаллах и солитоны, к-рые в том или ином виде существуют во всех упомянутых средах.
Н. у. м. ф. возникают также как результат применения приближения Хартри - Фока к многочастичным квантовомеханич. системам и имеют в этом качестве применения в атомной и ядерной физике. Ещё одним источником Н. у. м. ф. является хим. физика. Это- Н. у. диффузии, описывающие волны горения и детонации, а также колебат. хим. реакции (см. Автоволны). К ним примыкают возникшие в биофизике ур-ния, описывающие распространение импульса по нервному волокну. Ур-ния этих типов возникают в задачах о самоорганизации (см. Синергетика )и диссипативных структурах.
Н. у. м. ф. играют важную роль и в фундам. физике, напр. ур-ния Эйнштейна для гравитац. поля (см. Тяготение). Ур-ния Эйнштейна в вакууме имеют ясный геом. смысл, описывая римановы пространства, Риччи тензор к-рых равен нулю. Геом. интерпретацию имеют и мн. Н. у. в квантовой теории поля, в частности Ян-га - Миллса поля.
Локализов. решения Н. у. м. ф. в квантовой теории поля можно рассматривать как точки стационарной фазы при квазиклассич. вычислении функциональных интегралов, для Грина функций, содержащих информацию о спектре масс и сечениях взаимодействия элементарных частиц. Если точкам стационарной фазы соответствуют траектории подбарьерных переходов между топологически неэквивалентными вырожденными состояниями вакуума, классич. Н. у. м. ф. следует рассматривать в мнимом времени, т. е. не в пространстве Минковского, а в четырёхмерном евклидовом пространстве. Локализов. решения таких ур-ний - четырёхмерные солитоны - получили назв. инстантонов. Ур-ния Янга - Миллса описывают частицы, обладающие асимптотической свободой. В двумерном пространстве-времени этим же свойством обладает ур-ние n -поля:
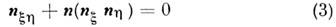
(здесь x = х+ t,h= x - t -"конусные" переменные). Это ур-ние является частным случаем более общего ур-ния "главного кирального поля"
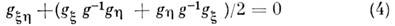
(здесь g - элемент нек-рой группы Ли). Инстантон-ные решения этого ур-ния можно использовать для описания солитонных конфигураций в жидком гелии.
Универсальные модели. В этих моделях проявляется одна из характерных черт теории Н. у. м. ф.: среди огромного их многообразия можно выделить небольшое число ур-ний сравнительно простого вида, к-рые можно использовать как матем. модели различных по своей природе физ. ситуаций. Эти ур-ния играют, в известном смысле, ту же роль, что и классич. ур-ния в частных производных (ур-ние Лапласа, ур-ние диффузии, волновое ур-ние).
К числу таких универсальных моделей относятся Кортевега - де Фриса уравнение, Шрёдингера уравнение нелинейное, синус-Гордона уравнение, Кадомцева - Петвиашвили уравнение, Вюргерса уравнение, Хохло-ва - Заболотской уравнение и др. Необходимо отметить еще систему ур-ний "трёх волн":
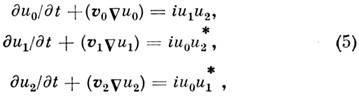
являющуюся универсальной моделью для описания па-раметрич. взаимодействий волн в нелинейных средах. Система (5) допускает многочисл. обобщения.
Большое разнообразие встречающихся в физике Н. у. и. ф. затрудняет развитие общих матем. методов их исследования. Лишь для сравнительно немногих Н. у. м. ф. доказаны теоремы существования и единственности, к таким относятся ур-ния Янга - Миллса, ур-ния Навье - Стокса в двумерном случае, ур-ния газовой динамики. Для ур-ний Навье - Стокса в трёхмерном случае теорема единственности решения задачи Коши до сих пор не доказана. Затруднена даже проблема классификации Н. у. м. ф. Часть их попадает под классич. разделение на эллиптич., гиперболич. и параболич. ур-ния, но значит. число важных Н. у. м. ф. (среди них Кортевега - де Фриса ур-ние, Кадомцева - Петвиашвили ур-ние) не могут быть отнесены ни к одному из этих типов. Нек-рую классификацию Н. у. м. ф. можно осуществить на основе физ. соображений. Прежде всего это разделение на стационарные и эволюц. ур-ния. Большинство стационарных ур-ний относится к эллиптич. типу. Среди эволюц. ур-ний, явно содержащих производные по времени, можно выделить консервативные Н. у. м. ф., сохраняющие интеграл энергии, и диссипативные Н. у. м. ф., описывающие "открытые системы", обменивающиеся энергией с "внешним миром". Одним из интересных достижений теории Н. у. м. ф. было обнаружение того факта, что консервативные Н. у. м. ф., как правило, являются га-мильтоновыми системами, хотя явное введение кано-нич. переменных зачастую оказывается трудной задачей. Установлена гамильтонова природа большинства консервативных обобщений ур-ний Эйлера и даже системы ур-ний Власова, описывающих плазму без столкновений. Для гамильтоновых систем, близких к линейным, развиты методы теории возмущений, позволяющие учитывать нелинейные эффекты и производить статистич. описание решений.
Все перечисленные выше универсальные Н. у. м. ф., за исключением Бюргерса ур-ния и Хохлова - Заболотской ур-ния, являются гамильтоновыми. Точные решения. Для физики важно знать как можно больше точных решений Н. у. м. ф., особенно существенно нелинейных. Простейшие из таких решений можно находить, используя очевидные свойства симметрии Н. у. м. ф., а также отыскивая всевозможные автомодельные подстановки (см. Автомодельностъ). Более тонкие способы вычисления точных решений используют методы теории групп Ли. Пусть Н. у. м. ф. для ф-ции двух переменных u(x,t )имеет вид
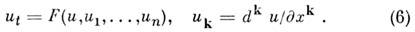
Ф-ция
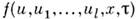 наз. симметрией уравнения (6), если оно совместно с ур-нием ut = =
наз. симметрией уравнения (6), если оно совместно с ур-нием ut = = 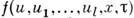 , где t - новая переменная. Симметрии образуют алгебру Ли относительно скобки Пуассона
, где t - новая переменная. Симметрии образуют алгебру Ли относительно скобки Пуассона 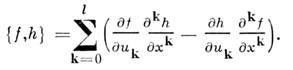
По алгебре симметрии Н. у. м. ф. восстанавливают группу Ли - Беклунда непрерывных преобразований, оставляющих Н. у. м. ф. инвариантным. Точные решения Н. у. м. ф. находят как решения, остающиеся инвариантными при действии к.-л. подгруппы группы Ли - Беклунда. Группа Ли - Беклунда и алгебра симметрии существуют у каждого Н. у. м. ф. В большинстве случаев группа Ли - Беклунда является конечномерной. Существуют, однако, случаи, когда эта группа бесконечномерна, как у всех перечисленных выше универсальных Н. у. м. ф.
Если преобразование из группы Ли - Беклунда оставляет инвариантным функционал действия гамиль-тонова Н. у. м. ф., то оно имеет интеграл движения - функционал, не зависящий от времени. Интегралы движения образуют алгебру Ли относительно скобок Пуассона, изоморфную нек-рой подалгебре алгебры симметрии.
Перечисленные выше универсальные гамильтоновы Н. у. м. ф. обладают бесконечными наборами независимых интегралов движения. Ур-ния, обладающие этим свойством, несколько условно наз. интегрируемыми, хотя интегрируемость (см. Гамильтонова система )доказана лишь для немногих из них. Интегрируемыми являются, в частности, одномерные ур-ния Эйлера (2).
Обширный класс интегрируемых Н. у. м. ф. составляют ур-ния, к к-рым применим обратной задачи рассеяния метод. Для этих ур-ний, к к-рым относятся, в частности, перечисленные выше универсальные гамильтоновы системы, возможно явное вычисление большого кол-ва точных решений, в т. ч. описывающих солитоны и их взаимодействия. При помощи метода обратной задачи удаётся вычислять инстантонные решения ур-ний Ян-га - Миллса, а также найти многочисленные точные решения ур-ний Эйнштейна.
Если Н. у. м. ф. не обладает бесконечной группой Ли - Беклунда, возможности его аналитич. исследования сильно ограничены. В ряде случаев можно, используя разложение по набору заданных ф-ций (метод Галеркина), свести его к системе обыкновенных диф-ференц. ур-ний, к-рую можно изучать качеств. методами, а также интегрировать при помощи ЭВМ. Таким способом удаётся моделировать не слишком развитую турбулентность, в т. ч. изучать странные аттракторы. Наконец, если число независимых переменных, входящих в Н. у. м. ф., не превышает три, оказывается достаточно эффективным их прямое численное решение на ЭВМ.
Лит.: Уизем Д ж., Линейные и нелинейные волны, пер. с англ., М., 1977; Теория солитонов. Метод обратной задачи, М., 1980; Ablowitz М. J., Segur H., Solitons and the inverse scattering transform, Phil., 1981;Ибрагимов Н. <Х., Группы преобразований в математической физике, М., 1983.
В. Е. Захаров.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
