СТОХАСТИЧЕСКИЕ КОЛЕБАНИЯ

СТОХАСТИЧЕСКИЕ КОЛЕБАНИЯ

(от греч. stochastikos - умеющий угадывать)- нерегулярные, внешне неотличимые от реализации случайного процесса колебанияв полностью детерминированной (без шумов и флуктуации) нелинейной системе.

Сложное поведение нелинейных колебат. систем наблюдалось (1920-е - 50-егг.) задолго до осознания факта возможности существования стохастичностив таких системах (эксперименты Ван дер Поля и Ван дер Марка [1], двухдисковоединамо [2], распределённая система авторегулирования темп-ры [3]). Крометого, хотя в то время существовали нек-рые элементы матем. аппарата дляописания нетривиального поведения траекторий динамических систем вфазовом пространстве (гомоклинич. структуры Пуанкаре [4]), однако представленияо том, что детерминиров. системы могут вести себя хаотически, ещё не прониклини в физику, ни в математику. Качественное изменение ситуации произошлов 1960-е гг. в связи с открытиями в математике [5-6] и компьютерными исследованиямимоделей физ. систем.

С. к., как и истинно шумовые колебания, характеризуются сплошным Фурьеспектром и спадающей автокорреляц. ф-цией (см. Хаос). Отличаетих от случайных флуктуации то обстоятельство, что они могут генерироватьсядинамич. системой с конечным числом степеней свободы (в то время как генерацияшума требует от системы возбуждения бесконечного числа независимых степенейсвободы). Физ. природа возникновения сложного запутанного поведения конечномернойсистемы связана с неустойчивостью всех (или большинства) индивидуальныхдвижений. Неустойчивость траекторий, располагающихся в органич. областифазового пространства, и приводит к перемешиванию, следствием к-рого являетсязапутанность, сложность, стохастичность движения. Важными характеристикамиэтой сложности и запутанности являются фрактальная размерность предельногомножества ( странного аттрактора) А и топологич. энтропия системына нём (см. Фракталы).

Выберем на странном аттракторе ансамбль из отрезков траекторий длительности Т, отстоящих друг от друга на расстояние 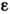.Предположим, что любой отрезок длительности Т произвольной траекториив аттракторе лежит в 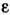-окрестностихотя бы одного из отрезков. Обозначим через С 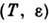числоотрезков (элементов) в ансамбле. При уменьшении 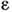или увеличении Т число С 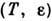увеличивается. <Рост С 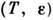приубывании 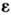естественносвязан с геом. сложностью аттрактора. Увеличение же С 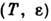привозрастании Т есть следствие неустойчивости траекторий в аттракторе. <Рассмотрим следующие характеристики движения на аттракторе;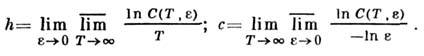

Величину h наз. топологич. энтропией, с - фрактальнойразмерностью аттрактора. Сигналу (реализации, наблюдаемой), с к-рым имеетдело исследователь, в эффективном фазовом пространстве (возможно, бесконечномерном)исследуемой системы отвечает предельное множество соответствующих траекторий. <Его размерность естественно называть размерностью реализации, а топологич. <энтропию системы, рассматриваемой лишь на этом предельном множестве, можноназвать топологич. энтропией реализации. Существуют алгоритмы определенияэтих величин, к-рые позволяют вычислить их для сигналов, генерируемых реальнымипроцессами [7] (течение жидкости, энцефалограммы и пр.). Конечность этихвеличин свидетельствует о динамич. характере исследуемого процесса, а самиони характеризуют «степень стохастичности» системы.

Стохастичность гамильтоновых систем. Стохастич. свойства демонстрируютдаже очень простые гамильтоновы системы, напр. маятник под действием внеш. <иериодич. силы:

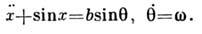
Фазовое пространство этой системы трёхмерно и очевидно, что нач. фазовыйобъём сохраняется. Если в такой системе (в определ. области параметров)рассмотреть каплю «фазовой жидкости» в пространстве {(х, х,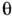)},то можно обнаружить, что через нек-рое время она, сложным образом деформируясь, <заполнит определ. область в фазовом пространстве, к-рая и будет соответствоватьстохастич. движениям (рис. 1).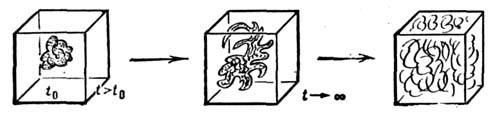

Рис. 1.

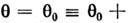
Однако наряду с этой областью перемешивания (или областью стохастичности)в фазовом пространстве (1) всегда будут существовать нач. условия, к-рымотвечает регулярное периодическое или квазипериодическое поведение. Особеннонаглядно это видно на секущей плоскости 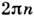(на рис. 2 показаны следы фазовых траекторий- траектории отображения Пуанкаре).Регулярным движениям отвечают двумерные торы, на к-рых лежат траектории, <соответствующие условно периодич. движениям (на рис. 2 - это замкнутыекривые). В области хаоса эти торы разрушены. Очевидно, в трёхмерном фазовомпространстве (и в четырёхмерном на трёхмерной поверхности пост. энергии)области хаотического и регулярного поведения разделены. Такие системы наз. <системами с разделённым фазовым пространством [8]. Если фазовое пространствоимеет размерность больше четырёх, то геом. запретов, гарантирующих разделениехаотических и регулярных движений, уже не существует и области стохастич. <поведения в разных частях фазового пространства могут соединяться другс другом отрезками одной и той же траектории. Обычно это происходит вдоль сепаратрис (стохастич. диффузия, или диффузия Арнольда [8]).

Возникновение стохастичности в гамильтоновых системах типа (1) определяетсязначением амплитуды внеш. силы, что имеет простой физ. смысл. При достаточнобольших амплитудах появляется большое число гармоник осн. частоты колебаний, <на каждой из к-рых возможен нелинейный резонанс; при дальнейшем увеличенииамплитуды области резонанса в фазовом пространстве, соответствующие этимдвижениям, перекрываются (т. н. перекрытие резонансов Чирикова). Обнаружениестохастич. поведения гамильтоновых систем, обладающего не только эргодичностью, но и более сильными статистич. свойствами (перемешиванием, спадениемавтокорреляц. ф-ции и т. п.), позволяет построить динамич. модели, на основек-рых могут быть получены осн. законы статистич. механики без предварит. <гипотез. Это - модели типа бильярда Синая [9], газа Лоренца [10] и пр.

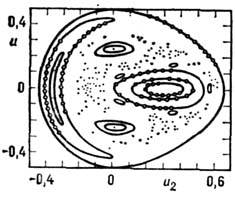
Рис. 2.

Стохастические автоколебания. В системах с диссипацией, напр. в системе

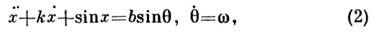
фазовый объём не сохраняется - он сжимается, поэтому можно было бы ожидать, <что движение системы может лишь упроститься. Однако стохастич. поведениев таких системах сохраняется; лишь незначительно (в зависимости от величины k )уменьшается размерность стохастич. множества, к-рое в данном случаеявляется странным аттрактором. Стохастич. автоколебания реализуютсяне только в простой модели (2) неавтономного осциллятора, но и практическив любой нелинейной колебательной диссипативной системе с периодич. силой, <если её амплитуда не слишком мала, даже если потенциал осциллятора имеетлишь один минимум (в фазовом пространстве невозмущённой системы одно положениеравновесия), как в системе, описываемой ур-нием

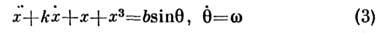
(нелинейный резонанс с учётом затухания). Существование стохастич. автоколебанийв системе

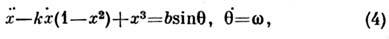
описывающей (с учётом нелинейной реактивности), в частности, синхронизациюколебаний, означает, кроме прочего, и то, что при переходе в области параметровчерез границу режима захватывания могут возникнуть не только биения, нои сложные колебания, ничем не отличимые от случайных. На рис. 3 приведеныаттракторы систем, описываемых ур-ниями (3) и (4) при соответствующих значенияхпараметров.

Движения на странном аттракторе - установившиеся стохастич. автоколебания. <Подобно периодич. автоколебаниям, матем. образом к-рых является предельныйцикл, осн. характеристики установившихся движений (спектр колебаний, размерность, <энтропия и др.) на странном аттракторе не зависят от нач. условий. Нач. <условия сказываются лишь на характере переходного процесса. Несмотря нато, что странный аттрактор состоит из неустойчивых траекторий, т. е. движениерядом с каждой из них происходит лишь конечное время, однако переходы содной неустойчивой траектории на другую происходят таким образом, что движениесистемы осуществляется вдоль траектории, тоже принадлежащей странному аттрактору[11].

В многомерных системах размерность странных аттракторов может быть многоменьше размерности фазового пространства, что соответствует частичной синхронизациистепеней свободы системы.

Пути возникновения стохастических колебаний [12, 13]. Последовательности бифуркаций (сценарии, пути), приводящие к возникновению С. к. при изменении параметровсистемы, могут быть бесконечно разнообразны, однако элементарных бифуркацийили их последовательностей, содержащихся в этих сценариях, не так много.

Рассмотрим вначале режимы «мягкого» возникновения стохастич. автоколебаний. <Осн. бифуркации в этом случае представлены на рис. 4. Это - рождение тораиз предельного цикла при потере им устойчивости, бифуркация удвоения периода, <слияние устойчивого и седлового циклов и их исчезновение, сопровождающеесявозникновением странного аттрактора, сложные деформации («гофрирование»)тора и его разрушение, сопровождающееся возникновением большого числа гармоники субгармоник в спектре колебаний. Для «жёсткого» режима возникновенияС. к. характерно превращение непритягивающих гомоклинич. структур в фазовомпространстве, образовавшихся в результате потери устойчивости простымиаттракторами, в странный аттрактор.

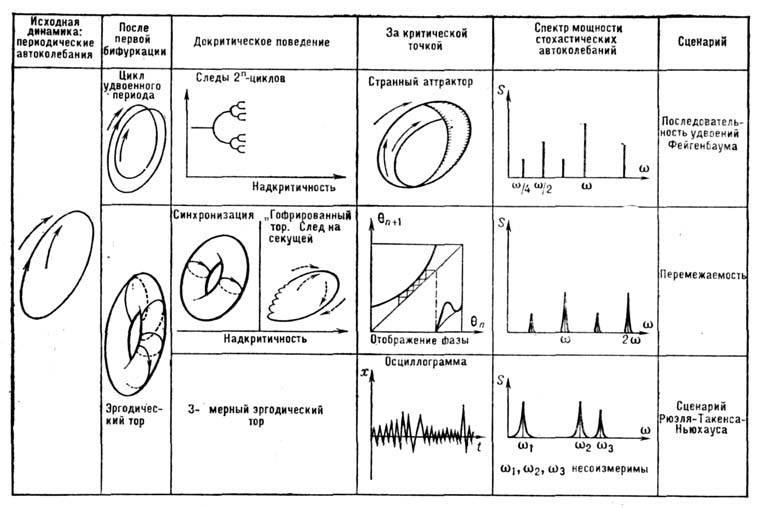
Рис. 3.

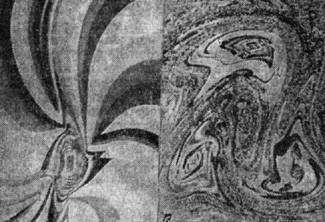
Рис. 4.

Стохастические колебания в распределённых системах [14] - неупорядоченноеповедение не только во времени, но и в пространстве. Степень неупорядоченностиэтих движений связана с числом независимых степеней свободы, формирующихэто движение.

Пример подобного неупорядоченного движения распределённой гамильтоновойсистемы - стохастич. движение солитона, описываемое нелинейным Шрёдингерауравнением с гармонич. потенциалом:

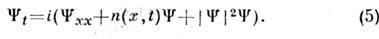
Для «медленных» переменных, определяющих координаты центра солитона, <в одномерной ситуации получается ур-ние движения, совпадающее с (1). Т. <о., один из механизмов стохастизации волнового поля связан с формированиемлокализов. образования (солитона) и его хаотич. блуждания в физ. пространстве, <подобного нерегулярному движению изображающей точки в фазовом пространственелинейного осциллятора (1).

В диссинативных распределённых системах незатухающие С. к. возможнылишь при наличии источника энергии (потоки массы или тепла в гидродинамич. <течениях, накачка в лазерах, пост. или периодич. магн. поле при возбужденииспиновых волн и т. д.). Установившиеся стохастич. пульсации в распределённойдиссипативной системе, к-рым соответствуют конечномерные аттракторы, естьстохастич. автоколебания. При не слишком больших числах Рейнольдса чертыгидродинамич. турбулентности описываются движениями на конечномерномстранном аттракторе, размерность к-рого обычно растёт с ростом числа Рейнольдса.

Лит.:l)Van der Pol В., Van der MarkJ., Frequency demultiplication,«Nature», 1927, v. 120, p. 363; 2) R i k i t a k e Т., Oscillations ofa system of disc dynamics, «Proc. Camb. Philos. Soc.», 1958, v. 54, № 1,p. 89; 3) Алексеев А. С., Двухпо:шционный регулятор температуры с зонойопережения, в сб.: Памяти А. А. Андронова, М., 1955; 4) П у а н кар е А.. Избр. труды, т. 2, М., 1972; 5) А н о с о в Д. В., Геодезическиепотоки на замкнутых римановых многообразиях отрицательной кривизны, «Тр. <Мат. ин-та АН СССР», 1967, т. 90; 6) Синай Я. Г., Марковские разбиенияи У-диффеоморфизмы, «Функциональный анализ и его приложения», 1968, т.2, в. 1, с. 64; 7) Р а б и н о в и ч М. И., Сущик М. М., Регулярная и хаотическаядинамика структур в течениях жидкости, «УФН», 1990, т. 160, с. 3; 8) ЛихтенбергА., Либерман М., Регулярная и стохастическая динамика, пер. с англ., М.,1984; 9) Б у н и м о в и ч Л. А. и др., Эргодическая теория гладких динамическихсистем, в кн.: Итоги науки и техники. Современные проблемы математики. <Фундаментальные направления, т. 2, М., 1985; 10) С и н а й Я. Г., Ч е рн о в Н. И., Энтропия газа твердых сфер по отношению к группе пространственно-временныхсдвигов, в сб.: Труды семинара им. И. Г. Петровского, в. 8, М., 1982, с.218; 11) А л е к с е е в В. М., Якобсон М. В., Добавление. Символическаядинамика и гиперболические динамические системы, в кн.: Б о у э н Р., Методысимволической динамики, пер. с англ., М., 1979; 12) Рабинович М. И., ТрубецковД. И., Введение в теорию колебаний и волн, М., 1984; 13) Ш у с т е р Г.,Детерминированный хаос, пер. с англ., М., 1988; 14) Рабинович М. И., Стохастическиеавтоколебания и турбулентность, «УФН», 1978, т. 125, с. 123. В. С. Афраимович, <М. И. Рабинович.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.