СИНХРОНИЗАЦИЯ КОЛЕБАНИЙ

СИНХРОНИЗАЦИЯ КОЛЕБАНИЙ

       

установление и поддержание такого режима колебаний двух или неск. связанных систем, при к-ром их частоты равны, кратны или находятся в рациональном отношении друг с другом. В отсутствие взаимодействия частоты колебаний этих систем могут быть любыми. Различают взаимную С. к. связанных систем, при к-рой каждая из систем действует на другие и частота С. к. отличается от исходных частот, и принудительную С. к., или захватывание частоты, при к-рой связь между системами такова, что одна из них (синхронизирующая) влияет на другую (синхронизируемую), а обратное влияние исключено; в этом случае устанавливается колебание с частотой синхронизирующей системы. При взаимной С. к. двух связанных генераторов, сильно различающихся по мощности, более мощный генератор играет роль синхронизирующего, а менее мощный — синхронизируемого. Этот случай является переходным от взаимной С. к. к принудительной.

С. к. двух связанных систем, имеющих в отсутствие взаимодействия частоты w1 и w2, обычно происходит при значениях разности частот Dw=w1-w2, находящихся внутри определённого интервала. Ширину этого интервала наз. полосой синхронизации (захватывания). При С. к. двух автоколебательных систем полоса синхронизации тем меньше, чем слабее связь между системами.

Применения С. к. обширны. Так, С. к. позволяет генераторам переменного тока, синхронным моторам и др. нелинейным системам входить в синхронный режим и устойчиво работать в пределах конечной полосы частот, а также позволяет неск. генераторам устойчиво работать на общую сеть энергосистемы или неск. радиопередатчикам на одну антенну. С. к. используется при создании умножителей и делителей частоты. В сложных нелинейных системах, генерирующих неск. частот, возможна С. к. на различных комбинац. частотах системы. Напр., С. к. на разностной частоте применяется при синхронизации мод лазера. Больным с нарушением ритма сердца вживляют электронный синхронизатор сердечного ритма (т. н. кардиостимулятор). С. к. лежит в основе объяснения многих физ. явлений. Так, с классич. точки зрения вынужденное излучение физ. системы, состоящей из набора осцилляторов, есть результат С. к. этих осцилляторов коллективным полем излучения.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

СИНХРОНИЗАЦИЯ КОЛЕБАНИЙ

- согласование частот, фаз или др. характеристиксигналов, генерируемых взаимодействующими колебательными системами. Различаютвзаимную С. к., когда парциальные подсистемы перестраивают режим колебанийдруг друга, и внешнюю (вынужденную) С. к., когда характеристики колебанийсистемы (систем) изменяются под действием внеш. силы. Вынужденную синхронизациюпо частоте колебаний, т. е. навязывание системе, характеризующейся в автономномрежиме одной частотой колебаний, др. частоты, определяемой внеш. силой, <называют захватыванием частоты. Захватывание частоты - простейшийпример явления синхронизации, к-рый был описан ещё X. Гюйгенсом (Ch. Huygens)в связи с ускорением или замедлением хода часов, висящих на независимоколеблющейся балке (см., напр., [1]).

Наиб. полно развита теория С. к. для квазигармонических колебаний вслабо нелинейных системах [2-4].

В частности, усреднённые по периоду внеш. силы ур-ния для комплекснойамплитуды а нелинейного генератора с одной степенью свободы, находящегосяпод действием слабой гармонической силы, имеют вид:

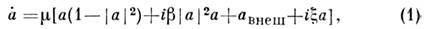
где 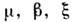- действительные параметры: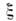- расстройка между частотой автоколебаний и частотой внеш. силы,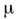- коэф. усиления в автономном генераторе,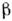- нелинейный сдвиг частоты. Режиму С. к. соответствует устойчивое положениеравновесия системы (1). В исходном же (3-мерном) фазовом пространстве режимуС. к. отвечает устойчивый предельный цикл. При увеличении 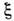режим С. к. либо перестаёт существовать (при слабых внеш. сигналах), либотеряет устойчивость (в случае сильных сигналов). Область значений расстроек, <для к-рых реализуется режим С. к., наз. полосой захватывания. Граница полосызахватывания находится из (1): из условия существования режима С. к. (а= 0) устанавливается резонансная кривая 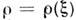, где 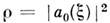- интенсивность автоколебаний в режиме С. к., и по линеаризованному ур-ниюопределяется устойчивость этого режима. На рис. 1 показаны полосы захватыванияв случаях слабых и сильных сигналов. На рис. 2 изображены последовательностифазовых портретов на плоскости (Rea, Ima),. отвечающих (1)при разных значениях расстройки. При переходе через границу области захватываниярежим С. к. сменяется режимом биений - наблюдается бифуркация Андронова - Хопфа (при сильных сигналах) или бифуркация рождения предельногоцикла из петли, сепаратрисы седло - узел (при слабых сигналах).В исходном (3-мерном) фазовом пространстве переходу к режиму биений отвечаетрождение притягивающего двумерного тора с квазипериодич. обмоткой. Аналогичнымобразом можно исследовать С. к. ансамбля генераторов, находящихся под действиемодной и той же внеш. гармонической силы [5, 6].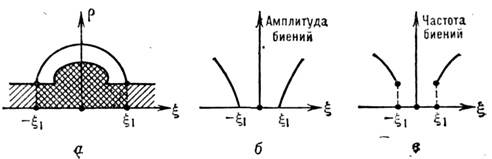

Рис. 1.

Рис. 2.

Явление взаимной синхронизации генераторов квазигармонических колебанийв простейшем случае бигармонического резонанса 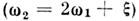может быть исследовано в рамках системы ур-ний для комплексных амплитуд а_1,2 взаимодействующих мод в автогенераторе с двумя степенямисвободы: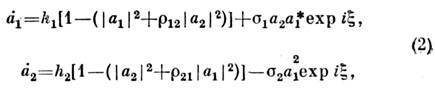

где 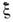- расстройка от точного резонанса, h_1,2 - инкрементыкаждой из мод,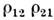- параметры, характеризующие конкуренцию мод, а 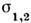- их резонансное взаимодействие. Здесь также режиму С. к. отвечает устойчивоесостояние равновесия, граница области устойчивости к-рого и определяетграницу области взаимной синхронизации [3]. Взаимная синхронизация наблюдаетсяв системах с числом степеней свободы 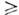2, и во многих ситуациях после разрушения режима С. к. возможно возникновениестохастических автоколебаний (см. Стохастические колебания). ЯвлениеС. к. наблюдается не только в случае, когда частоты парциальных генераторовблизки друг к другу, но и когда они близки к кратным друг друга (синхронизацияна гармониках и субгармониках). Именно за счёт взаимной синхронизации модоптич. резонатора удаётся реализовать режим генерации ультракоротких импульсовв лазерах [7].

В сильно нелинейном случае усреднённое описание, приводящее к ур-ниямтипа (1) и (2), не адекватно задаче, и здесь используется качеств. теориялинамических систем. В этой теории явление синхронизации периодич. колебанийдвух автоколебат. систем можно описать следующим образом. Каждой из системсвойственны периодич. автоколебания, т. е. в ее фазовом пространстве имеетсяустойчивый предельный цикл - L₁ и L₂ соответственно.

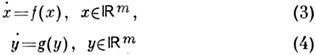
Система

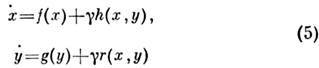
при 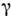= 0 будет иметь притягивающий двумерный тор 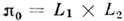(каждая система колеблется независимо от другой). При возрастании параметрасвязи 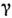движениев парциальных подсистемах системы (5) перестаёт быть независимым, что отвечаетбифуркациям на торе 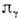[остающемся аттрактором для системы (5)]. В частности, явлению синхронизацииотвечает рождение устойчивого предельного цикла на этом торе.

Более подробную информацию о перестройках в системе при изменении параметрасвязи даёт т. н. дьявольская лестница - график зависимости числа вращениясистемы на торе 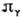от параметра связи. [Число вращения - это предел отношения фаз бывших независимымипри 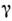=0 колебаний парциальных генераторов:

Зависимость 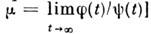числа вращения от величины параметра связи имеет вид непрерывно уменьшающихсяступеней (рис. 3). Точнее, ф-ция 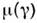растёт на канторовом множестве. Каждое своё значение, равное отношениюцелых чисел p/q (синхронизация), число вращения принимает, вообщеговоря, на нек-ром интервале, а числа р и q соответствуютномерам гармоник, на к-рых осуществляется взаимная синхронизация. Еслиследить за изменением не только параметра связи, но и др. параметра (напр.,надкритичности в каждом из генераторов), то области синхронизации будутизображаться уже не на прямой, а на плоскости. Обычно эти области имеютвид «языков» [8] (т. н. языки Арнольда [9]) - рис. 4.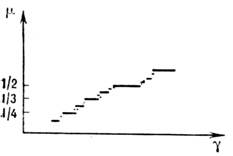

Рис. 3.

Рис. 4.

Рис. 5.

Взаимное согласование движений свойственно генераторам не только периодических, <но и стохастических автоколебаний. Принципиальное отличие от случая периодич. <колебаний здесь в том, что движения взаимодействующих неидентичных подсистемсогласуются лишь в среднем по времени. При этом могут быть одинаковымитопология проекций странных аттракторов на парциальные подпространства, <их размерности, спектры мощности парциальных колебаний. В то же время самиреализации локально по времени могут не совпадать. На рис. 5 представленыстранные аттракторы парциальных подсистем в автономном режиме (С = 0) ипроекции аттрактора на парциальные подпространства в режиме стохастич. <синхронизации ( С =10) для системы, описываемой ур-ниями вида:

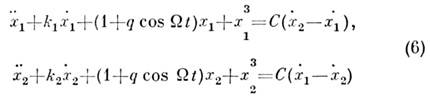
(напр.,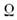= 2, k₁ =0,48, k₂ = 0,45 для двухсвязанных параметрически возбуждаемых генераторов [10]). Степень стохастич. <синхронизации может быть различной; в частности, в нек-рых ситуациях, когдавзаимодействуют идентичные подсистемы, совпадение парциальных колебанийможет быть полным.

Лит.:1) Блехман И. И., Синхронизация в природе и технике, М.,1981; 2) Андронов А. А., В и т т А. А., К математической теории захватывания, <в кн.: А н д р о н о в А. А., Собр. трудов, М., 1956; 3) Блакьер О., Анализнелинейных систем, пер. с англ., М., 1969; 4) Рабинович М. И., ТрубецкойД. И., Введение в теорию колебаний и волн, М., 1984; 5) A i z a w a Y.,Synergetic approach to the phenomena of mode-locking in nonlinear systems,«Progr. Theor. Phys.», 1976, v. 56, № 3, p. 703; 6) Рабинович М. И., Стохастическиеавтоколебания и турбулентность, «УФН», 1978, т. 125, с. 123; 7) Квантоваярадиофизика, 2 изд., т. 2 - X а н и н Я. И., Динамика квантовых генераторов, <М., 1975; 8) Арнольд В. И., Малые знаменатели: 1. Об отображениях окружностина себя, «Изв. АН СССР. Сер. мат.», 1961, т. 25, с. 21; 9) Т h о m р sо n J. М., S t e w a r t H. В., Nonlinear dynamics and chaos, N. Y.- [a.o.], 1986; 10) А ф р а й м о в и ч В. С., В е р и ч е в Н. Н., РабиновичМ. И., Стохастическая синхронизация колебаний в диссипативных системах,«Изв. вузов. Радиофизика», 1986, т. 29, № 9, с. 1050. В. С. Афраймович, <М. И. Рабинович.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.