НЕЛИНЕЙНЫЕ СИСТЕМЫ

НЕЛИНЕЙНЫЕ СИСТЕМЫ

       

колебательные системы, св-ва к-рых зависят от происходящих в них процессов. Колебания таких систем описываются нелинейными ур-ниями. Нелинейными явл.: механич. системы, где модули упругости тел зависят от деформаций последних или коэфф. трения между поверхностями тел зависят от относительной скорости этих тел (скорости скольжения); электрические системы, содержащие сегнетоэлектрики, диэлектрич. проницаемость к-рых зависит от напряжённости электрич. поля, и т. д. Указанные зависимости в механич. системах приводят соответственно либо к нелинейности связей между напряжениями и деформациями (нарушению), либо к нелинейной зависимости сил трения от скорости скольжения, либо к нелинейной связи между действующей на тело силой и сообщаемым ему ускорением (если при этом скорость тела меняется по величине). Аналогично в электрич. системах оказываются нелинейными: связь между электрич. зарядами и напряжённостью создаваемого ими поля; связь между напряжением на концах проводника и силой протекающего по нему тока (нарушение закона Ома); связь между силой тока и напряжённостью создаваемого им магн. поля (магн. индукцией) в магнетике и др. Каждая из этих нелинейных связей приводит к тому, что дифференциальные ур-ния, описывающие поведение Н. с., оказываются нелинейными, откуда и назв. Н. с.

Все физ. системы явл. Н. с. Поведение Н. с. существенно отлично от поведения линейных систем. Одна из наиболее характерных особенностей Н. с.— нарушение в них суперпозиции принципа. Искажение в Н. с. формы гармонич. внеш. воздействия и неприменимость к Н. с. принципа суперпозиции позволяют осуществлять с их помощью генерирование и преобразования частоты эл.-магн. колебаний — выпрямление, умножение частоты, модуляцию колебаний и т. д.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

НЕЛИНЕЙНЫЕ СИСТЕМЫ

- колебательные (волновые) системы, процессы в к-рых не удовлетворяют суперпозиции принципу, в отличие от линейных систем. Все реальные физ. системы нелинейны, их можно считать линейными лишь приближённо -при малой интенсивности колебат. и волновых процессов. Матем. образом Н. с. являются нелинейные ур-ния (см. Нелинейные уравнения математической физики). Изучением колебат. и волновых процессов в конкретных Н. с. занимаются гидродинамика, нелинейная оптика, нелинейная акустика, физика плазмы (см. Нелинейные явления в плазме), а также химия, биология, экология, социология и др. В то же время многие Н. с. совершенно различной природы имеют одинаковое матем. описание. Соответственно, совпадает и характер протекающих в них процессов. Это послужило основой для развития единого подхода к изучению Н. с., позволило выработать базовые модели, образы и понятия и проанализировать осн. колебат. и волновые явления в Н. с. вне зависимости от их конкретной природы.

Аналитич. описание процессов в Н. с. затруднено ввиду отсутствия общих методов решения нелинейных ур-ний. Наиб. доступно изучение динамики слабонелинейных систем. Описывающие их ур-ния содержат нелинейные члены с малым параметром, что позволяет использовать разл. варианты метода возмущений (см. Возмущений теория). Нелинейность в таких системах проявляется либо в возникновении малых поправок к решению линеаризов. системы ур-ний, получаемой в пренебрежении нелинейными членами, либо, что более важно, в медленном изменении его параметров. При исследовании сильнонелинейных систем, за исключением ограниченного числа точно решаемых случаев, используется численное моделирование.

Разделяют два класса Н. с.- консервативные системы, в к-рых энергия колебательных (волновых) процессов сохраняется, и неконсервативные системы, в к-рых энергия диссипирует ( диссипативиые системы )или поступает в систему от внеш. источников (активные системы). Прогресс в изучении консервативных Н. с. в значит. мере обусловлен возможностью применения к большинству из них аппарата гамильтонова формализма. Во многих практически важных случаях гамильтониан Н. с. совпадает с выражением для энергии системы. Известны, однако, консервативные Н. с., для к-рых га-мильтоново описание не построено. Для биол., эколо-гич., социологич. и т. п. И. с., в к-рых строгое определение консервативности с использованием интеграла энергии не применимо, также принято указанное деление, основанное на аналогии их описания с физ. Н. с.

Консервативные Н. с. Простейшим примером поведения консервативной Н. с. являются колебания нелинейного осциллятора, описываемые ур-нием

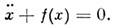
Если ф-ция f(x) линейна [f(x)- х], то осциллятор линейный. Ур-ние нелинейного осциллятора описывает, напр., колебания матем. маятника, изменения тока и напряжения в колебат. контуре, в к-ром индуктивность катушки зависит от величины тока и (или) ёмкость конденсатора зависит от напряжения, а также движение иона в пространственно неоднородном электрич. поле и др.

Рис. 1. Потенциал электрического поля j(x) и фазо вые траектории, отвечающие движению иона в дан ном поле при различных значениях энергии .

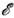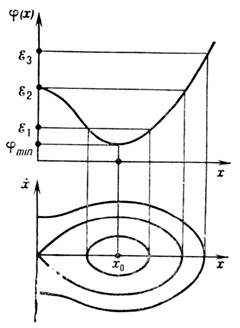
На рис. 1 приведены вид потенциального рельефа j(x) и соответствующие ему фазовые траектории - траектории движения изображающей точки Н. с. в фазовом пространстве ( х,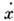). Энергия заряж. частицы, движущейся в стационарном электрич. поле, сохраняется: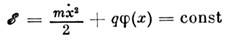

(где т,q - масса и заряд частицы; q > 0). Это выражение определяет гамильтониан осциллятора. Дифференцирование его по времени даёт ур-ние нелинейного осциллятора, где f(x)= q/mj'_x . Осциллятор является линейным лишь при условии j(x) ~ х², т. е. при пара-болич. потенциальном рельефе. При этом его колебания являются гармоническими и изохронными - их частота не зависит от амплитуды. Как видно из рис. 1, осциллятор имеет два состояния равновесия ( 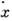= 0):

центр (при х = х₀ )и седло (при х =0), первое из них устойчиво (локальный минимум потенц. энергии), второе неустойчиво. Выведенная из состояния покоя при х = х₀. частица совершает колебания в окрестности этой точки (замкнутые кривые на рис. 1). При малых отклонениях х от х₀ осциллятор является линейным, т. к. j - j _мин ~ ( х -x₀)² при х - х₀.0. С ростом энергии осциллятора 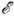фазовая траектория приближается к сепаратрисе. Колебания осциллятора становятся ангармоническими (возникают гармоники осн. частоты), т. к. всё большую часть периода занимают участки медленного движения частицы. Период колебаний возрастает с ростом их амплитуды и на сепаратрисе равен бесконечности (частица приближается к неустойчивому состоянию равновесия с бесконечно малой скоростью бесконечно долго). Т. о., колебания нелинейного осциллятора неизохронны - их период зависит от амплитуды (энергии).

В отличие от линейных систем, в Н. с. возможно взаимодействие колебаний (или волн) между собой. Такое взаимодействие имеет, напр., место в системе трёх нелинейно связанных осцилляторов, описываемой системой ур-ний

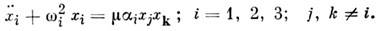
При малом m - это слабонелинейная система. Поведение её близко к суперпозиции квазигармонич. колебаний осцилляторов с медленно меняющимися амплитудами. Благодаря нелинейной связи колебания двух осцилляторов с частотами w₁. и w₂ порождают в системе колебания с комбинац. частотами w₁ bw₂. Действие малой нелинейности накапливается, если выполнено условие резонанса частот

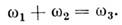
Эфф. обмен энергией между осцилляторами происходит, когда возбуждён ВЧ-осциллятор и энергия колебаний передаётся двум НЧ-осцилляторам - т. н. распадная неустойчивость, либо когда возбуждены два НЧ-осциллятора и идёт обратный процесс - слияние НЧ- колебаний. Подобный обмен энергией может быть периодическим (рис. 2). К задаче о взаимодействии нелинейно связанных осцилляторов сводятся во мн. случаях задачи о взаимодействии квазимонохроматич. волн в безграничных Н. с., таких, как линии передачи и волноводы с нелинейными элементами, нелинейные среды и т. п. В Н. с. с дисперсией волн эффективно взаимодействует ограниченное число волн, связанных с условиями резонанса частот и волновых векторов - условиями синхронизма.

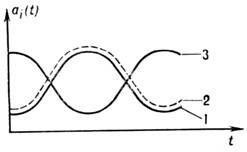
Рис. 2. Изменение амплитуд колебаний трёх вза имодействующих осцилляторов (w₃> w₁, w₂).

Рис. 3. Дисперсионные зависимости ионно-зву ковых (1 )и ленгмюровских (2) волн в плазме и диаграмма, иллюстрирующая условия синхронизма трёх взаимодействуюших волн.

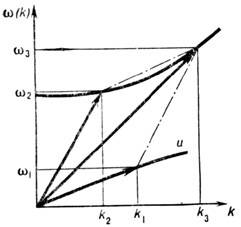
Для случая трёх взаимодействующих волн, напр. ионнозвуковой и ленгмюровских волн в плазме (см. Взаимодействие волн в плазме), они имеют вид (рис. 3):

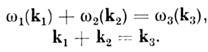
Как и при взаимодействии нелинейно связанных осцилляторов, здесь возможны распадная неустойчивость и слияние волн.

В отсутствие дисперсии волн в Н. с. в синхронизме с исходной квазимонохроматич. волной находятся все её гармоники. Поэтому если исходная волна гармоническая, то она порождает за счёт нелинейности гармоники с кратными частотами и волновыми числами, причём с течением времени возбуждаются всё более высокочастотные гармоники.

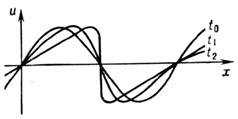
Рис. 4. Эволюция профиля исходной гармонической волны в отсутствие дисперсии волн (t₀<t₁<t₂).

На пространственно-временном языке этот процесс соответствует искажению профиля исходного возмущения (рис. 4) и описывается ур-нием простой волны

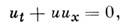
к-рое отвечает, в частности, нелинейным акустич. волнам в системе отсчёта, движущейся со скоростью звука малой амплитуды и отражает зависимость скорости распространения возмущения от его интенсивности. Решением его являются простые волны (или Рима-на волны) и = U(t - х/и), вид ф-ции U задаётся нач. возмущением. При и> 0 точки профиля с течением времени сдвигаются в направлении распространения волны, а при и <0 - в противоположном. Профиль волны искажается, и в нек-рый момент времени величина и _х становится бесконечной - происходит "опрокидывание" волны. Применимость ур-ния нарушается.

Наличие дисперсии волн в области ВЧ стабилизирует "опрокидывание", т. к. ВЧ-гармоники выходят из синхронизма и практически не возбуждаются. В результате противодействия нелинейности и дисперсии в безграничной Н. с. могут возникать т. н. стационарные волны, распространяющиеся с пост. скоростью без изменения формы профиля: периодич. волны сложной формы и уединённые волны - солитоны.

Наряду с взаимодействием волн в Н. с. важную роль играют эффекты самовоздействия. Если в Н. с. в силу особенностей дисперсионных характеристик условия трёхволнового взаимодействия не выполнены, то наиб. существенным является самовоздействие квазимонохроматич. волны. Оно возникает, напр., при распространении эл.-магн. волны в среде с показателем преломления, зависящим от интенсивности поля. В частности, пучок света в такой среде формирует неоднородное поперёк пучка распределение показателя преломления, подобное линзе, что в свою очередь может приводить к его фокусировке - происходит самофокусировка света. Аналогично возникают самомодуляция квазимонохроматич. волн в направлении их распространения и самосжатие волновых пакетов, приводящее к образованию стационарных волн огибающих нелинейных волновых пакетов, в т. ч. солитонов.

В Н. с. даже в отсутствие случайных воздействий возможны чрезвычайно сложные, нерегулярные коле-бат. и волновые режимы, требующие для своего описания привлечения вероятностных методов, - т. н. стохастические колебания. Такие колебания может совершать, напр., частица в двумерном потенц. поле при нек-рых формах потенц. рельефа. Стохастическим является также взаимодействие квазимонохроматич. волн в нелинейной среде, когда возбуждено много волн и каждая из них участвует во мн. элементарных взаимодействиях, удовлетворяющих условиям синхронизма,- т. н. слабая турбулентность (см. Турбулентность плазмы).

Неконсервативные Н. с. Наиб. простое проявление диссипации в системе - затухание колебат. и волновых процессов. Однако в безграничной Н. с. благодаря диссипации существует режим, отсутствующий в консервативных Н. с.,- ударные волны, в т. ч. стационарные ударные волны, имеющие вид бегущего перепада (скачка) к.-л. физ. параметров, напр. давления в аку-стич. ударной волне. Ударные волны возникают как результат эволюции простых волн: энергия ВЧ-гар-моник, генерируемых за счёт нелинейности, эффективно поглощается и "опрокидывания" волны не происходит.

В прикладном отношении наиб. важны нелинейные эффекты в активных Н. с., в к-рых энергия колебаний может пополняться вследствие неустойчивостей, обусловленных неравновесностью системы. К таким Н. с. относятся прежде всего генераторы колебаний - от лампового до квантовых (мазеров и лазеров), часы - от ходиков до кварцевых и т. п., в к-рых устанавливаются устойчивые незатухающие колебания с периодом и амплитудой, в широких пределах не зависящими от нач. условий,- автоколебания. Простейший генератор автоколебаний - автогенератор на ламповом триоде, в к-ром потери энергии в колебат. контуре компенсируются пополнением её за счёт непериодич. источника (батареи). Поступление энергии в контур в нужной фазе колебаний осуществляется при помощи обратной связи на управляющий электрод лампы. При перестройке параметров Н. с. могут происходить качественные изменения её поведения - бифуркации. Например, колебания в ламповом генераторе возникают при величине обратной связи, большей нек-рого бифуркационного значения.

Как и колебания в консервативных Н. с., колебания в активных Н. с. могут быть не только регулярными, но и стохастическими. Существуют генераторы стоха-стич. автоколебаний - Н. с., в к-рых возможны незатухающие хаотич. колебания со сплошным спектром за счёт энергии нешумовых источников. Самозарождение в Н. с. стохастич. колебаний - один из возможных путей возникновения турбулентности.

В активных колебат. Н. с., в к-рых возможно одно-врем. существование мн. мод (типов) колебаний с разл. частотами, получающих энергию от общего источника, возникает явление конкуренции мод, т. к. связь между модами порождает зависимость нелинейного затухания или усиления каждой из мод от интенсивности других. Конкуренция мод приводит к тому, что в итоге превалирует одна из них и колебания автогенератора происходят на соответствующей ей частоте. Если моды равноправны и связь их взаимна, то устанавливается режим генерации моды, преобладавшей вначале. В таких Н. с., как, напр., лазер, конкуренция мод происходит и во времени, и в пространстве, что приводит, в частности, к установлению в пространственно-симметричном протяжённом автогенераторе несимметричных в пространстве распределений поля с преобладанием одной из встречных волн. Это один из простейших примеров самоорганизации в Н. с.- возникновение пространственного порядка из нач. беспорядка и образование сложных пространственных структур в однородных (протяжённых) неравновесных Н. с. (физ., хим., биологических и т. п.). Примерами самоорганизации в Н. с. являются конвективные ячейки жидкости, подогреваемой снизу, волны горения, волны популяций в экологич. системах, волновые возбуждения в сердечной ткани.

Лит.: Андронов А. А.,Витт А. А., Xайкин С. Э., Теория колебаний, [3 изд.], М., 1981; Горелик Г. С., Колебания и волны, 2 изд., М., 1959; Уизем Д ж., Линейные и нелинейные волны, пер. с англ., М., 1977; Рабинович М. И., Трубецков Д. И., Введение в теорию колебаний и волн, М., 1984. А. Н. Басович.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.