ПАРАБОЛИЧЕСКОГО ЦИЛИНДРА ФУНКЦИИ

ПАРАБОЛИЧЕСКОГО ЦИЛИНДРА ФУНКЦИИ
ПАРАБОЛИЧЕСКОГО ЦИЛИНДРА ФУНКЦИИ

-ф-ции, удовлетворяющие ур-нию

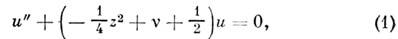
15035-26.jpg

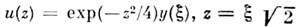
к-рое после замены 15035-27.jpg

переходит в уравнение Эрмита

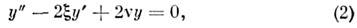
15035-28.jpg

где v - комплексный параметр.

Пусть 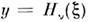15035-29.jpg- решение ур-ния (2), к-рое при v = п совпадает с полиномомЭрмита 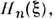15035-30.jpg п=0, 1,... (см. Ортогональные полиномы). П. ц. ф. Dv(z )равна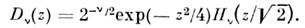

15035-31.jpg

Т. к. ур-ние (2) после замены 15035-32.jpgпереходит в ур-ние

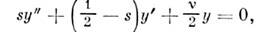
15035-33.jpg

решения к-рого можно выразить через вырожденныегипергеометрические функции F(a,c,x), то получаем

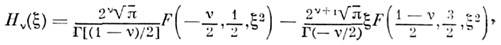
15035-34.jpg

где Г(t) - гамма-функция Эйлера. <Отсюда легко получить разложения в степенные ряды и асимптотич. представлениядля ф-ций Dv(z). Наряду с ф-цией Dv(z )ур-нию(1) удовлетворяют также ф-ции Dv( -z),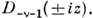15035-35.jpgФ-ции Dv(z )вещественны при вещественных v, z. П. <ц. ф. иногда наз. функциями Вебера. Для функции Эрмита 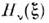15035-36.jpgимеются интегральное представление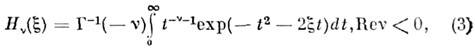

15035-37.jpg

ф-ла дифференцирования

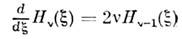
15035-38.jpg

и рекуррентное соотношение

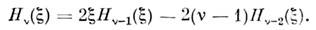
15035-39.jpg

Можно получить аналитич. продолжение ф-ции 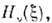15035-40.jpgопределяемой ф-лой (3), на область Re v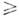15035-41.jpg0. Ур-ние (1) возникает, напр., при разделении переменных в волновом ур-нии, <записанном в цилиндрич. координатах, при рассмотрении гармонич. осцилляторав квантовой механике и в др. задачах.

Лит.: Бейтмен Г., Эрдейн А., Высшиетрансцендентные функции, пер. с англ., 2 изд., т. 2, М., 1974; НикифоровА. Ф., Уваров В. Б., Специальные функции математической физики, 2 изд.,М., 1984; Справочник по специальным функциям, пер. с англ., М., 1979.

А. Ф. Никифоров.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. . 1988.


.

Игры ⚽ Нужен реферат?

Полезное


Смотреть что такое "ПАРАБОЛИЧЕСКОГО ЦИЛИНДРА ФУНКЦИИ" в других словарях:

  • ПАРАБОЛИЧЕСКОГО ЦИЛИНДРА ФУНКЦИИ — Вебера функции, Вебера Эрмита функции, решения дифференциального уравнения к рое получается в результате разделения переменных в волновом уравнении в параболических ци линдрич. координатах. Наиболее часто используется решение где вырожденная… …   Математическая энциклопедия

  • Функции параболического цилиндра — (функции Вебера) общее название для специальных функций, являющихся решениями дифференциальных уравнений, получающихся при применении метода разделения переменных для уравнений математической физики, таких как уравнение Лапласа, уравнение… …   Википедия

  • Функции Бесселя — в математике  семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где   произвольное вещественное число, называемое порядком. Наиболее часто используемые функции Бесселя  функции целых… …   Википедия

  • Функции Эрмита — Функции параболического цилиндра общее название для специальных функций, являющихся решениями дифференциальных уравнений, получающихся при применении метода разделения переменных для уравнений математической физики, таких как уравнение Лапласа,… …   Википедия

  • Функции Ганкеля — (Ханкеля) (Функции Бесселя третьего рода) это линейные комбинации функций Бесселя первого и второго рода, а следовательно, решения уравнения Бесселя. Названы в честь немецкого математика Германа Ганкеля. функция Ганкеля первого рода; функция… …   Википедия

  • Специальные функции — встречающиеся в различных приложениях математики (чаще всего в различных задачах математической физики) функции, которые не выражаются через элементарные функции. Специальные функции представляются в виде рядов или интегралов. Специальные функции …   Википедия

  • ЭРМИТА ФУНКЦИИ — специальные функции, удовлетворяющие ур нию Эрмита (С. Hermit) Частные решения (1) имеют вид При целом v>0 Э. ф. совпадают с полиномами Эрмита (см. Ортогональные полиномы). Интегральное представление, ф лу дифференцирования и рекуррентное… …   Физическая энциклопедия

  • Цилиндрические функции — Цилиндрические функции  общее название для специальных функций одного переменного, являющихся решениями обыкновенных дифференциальных уравнений, получающихся при применении метода разделения переменных для уравнений математической физики,… …   Википедия

  • СПЕЦИАЛЬНЫЕ ФУНКЦИИ — в широком смысле совокупность отдельных классов функций, возникающих при решении как теоретических, так и прикладных задач в самых различных разделах математики. В узком смысле под С. ф. подразумеваются С. ф. математич. физики, к рые появляются… …   Математическая энциклопедия

  • Бесселевы функции — Функции Бесселя в математике  семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где α  произвольное действительное число, называемое порядком. Наиболее часто используемые функции Бесселя  функции целых… …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»