ИНТЕГРАЛЬНЫЙ ОПЕРАТОР

ИНТЕГРАЛЬНЫЙ ОПЕРАТОР
ИНТЕГРАЛЬНЫЙ ОПЕРАТОР

- обобщение понятия матрицы на бесконечно-мерный случай. Матрица Kij отображает векторы xj из векторного пространства X в векторы yi=Kijxj пространства Y. Простейший линейный И. о. определяется равенством
y(t)=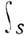008-115.jpgK(t,s)x(s)ds,
и отображает ф-ции x(s)из функциональногопространства X (области определения) в ф-ции y(t)из функционального пространства Y (область значений); ф-ция K(t, s) наз. ядром И. о. Чаще всего рассматривают И. о. на функциональных пространствах С (S )(непрерывных на замкнутом множестве S ф-ций) и Lp(S )(интегрируемых на S со степенью р ф-ций). Среди И. о. наиб, изучены (вполне непрерывные) фредгольмовы операторы. Ядро К при этом наз. фредгольмовым ядром. Напр., для И. о., действующего в C(S), ядро К фредгольмово, если ф-ция K(t, s )непрерывна в квадрате S3S. Для И. о. в L2(S )ядро фредгольмово, если выполнено неравенство: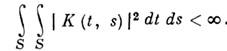
008-116.jpg
Важным частным случаем фредгольмова оператора является оператор Гильберта-Шмидта (см. Интегральное уравнение). Встречаются И. о. с полярным ядром (со слабой особенностью):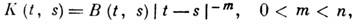008-117.jpgгде |t-s|- расстояние между точками s и t n -мерного пространства. Для ф-ций из С(S )И. о. с полярным ядром будет фредгольмовым, если ф-ция В (t, s )непрерывна на S3S; если В(t, s )ограничена всюду в квадрате S3S и
008-118.jpg
то И. о. с полярным ядром фредгольмов на L2(S). В матем. физике применяют разл. типы И. о., возникающих при интегральных преобразованиях. Лит.: Владимиров B.C., Уравнения математической физики, 5 изд., М., 1988: Интегральные уравнения, М., 1968; Рихтмацйер Р., Принципы современной математической физики, пер. с англ., М., 1982. С. В. Молодцов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. . 1988.


.

Игры ⚽ Поможем сделать НИР

Полезное


Смотреть что такое "ИНТЕГРАЛЬНЫЙ ОПЕРАТОР" в других словарях:

  • ИНТЕГРАЛЬНЫЙ ОПЕРАТОР — ИНТЕГРАЛЬНЫЙ ОПЕРАТОР, обобщение понятия матрицы (см. МАТРИЦА (в математике)) на бесконечномерный случай. Возникает при использовании интегральных преобразований …   Энциклопедический словарь

  • интегральный оператор — integralinis operatorius statusas T sritis fizika atitikmenys: angl. integral operator vok. Integraloperator, m rus. интегральный оператор, m pranc. opérateur intégral, m …   Fizikos terminų žodynas

  • ИНТЕГРАЛЬНЫЙ ОПЕРАТОР — отображение когда закон соответствия Азадается с помощью интеграла. И. о. наз. иногда интегральным преобразованием. Так, напр., для интегрального оператора Урысона (см. Урысона уравнение): закон соответствия Аопределяется интегралом (или оператор …   Математическая энциклопедия

  • ФУРЬЕ ИНТЕГРАЛЬНЫЙ ОПЕРАТОР — интегральный оператор, обобщенное ядро к рого является быстроосциллирующей функцией или интегралом от такой функции. Операторы такого типа возникли при исследовании асимптотики быстроосциллирующих решений уравнений с частными производными (см.… …   Математическая энциклопедия

  • Интегральный оператор Фредгольма — В математике интегральное уравнение Фредгольма  это интегральное уравнение, ядром которого является ядро Фредгольма. Названо так по имени изучавшего его Ивара Фредгольма. Со временем выросло в самостоятельный раздел функционального анализа … …   Википедия

  • ГИЛЬБЕРТА - ШМИДТА ИНТЕГРАЛЬНЫЙ ОПЕРАТОР — ограниченный линейный интегральный оператор Т, действующий из пространства в и представимый в виде где ядро оператора (см. [1]). Впервые такого рода операторы рассматривались Д. Гильбертом (D. Hilbert) и Э. Шмидтом (Е. Schmidt) в 1907. Г. Ш. и. о …   Математическая энциклопедия

  • Оператор (математика) — У этого термина существуют и другие значения, см. Оператор. Оператор (позднелат. operator  работник, исполнитель, от operor  работаю, действую)  то же, что отображение в математике. Термин оператор встречается в разных… …   Википедия

  • ПСЕВДОДИФФЕРЕНЦИАЛЬИЫЙ ОПЕРАТОР — оператор, действующий в функциональных пространствах на дифференцируемом многообразии и локально по определенным правилам записываемый с помощью нек poй функции, обычно наз. символом П. о., и удовлетворяющей оценкам производных определенного типа …   Математическая энциклопедия

  • Самосопряжённый оператор —         оператор, совпадающий со своим сопряжённым (см. Сопряжённые операторы). иначе называется эрмитовым. Теория С. о. возникла как обобщение теории интегральных уравнений с симметричным ядром, самосопряжённых дифференциальных уравнений,… …   Большая советская энциклопедия

  • ГИЛЬБЕРТА - ШМИДТА ОПЕРАТОР — оператор А, действующий в гильбертовом пространстве H такой, что для любого ортонормированного базиса в Нвыполнено условие: (достаточно, однако, справедливости этого для нек рого базиса). Г. Ш. о. является компактным оператором, для s чисел к… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»