ГИЛЬБЕРТА - ШМИДТА ОПЕРАТОР
- ГИЛЬБЕРТА - ШМИДТА ОПЕРАТОР
оператор А, действующий в гильбертовом пространстве H такой, что для любого ортонормированного базиса  в Нвыполнено условие:
в Нвыполнено условие:
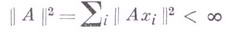
(достаточно, однако, справедливости этого для нек-рого базиса). Г.- Ш. о. является компактным оператором, для s-чисел к-рого 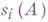 и для собственных чисел
и для собственных чисел 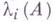 имеет место:
имеет место:
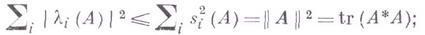
при этом  оказывается ядерным оператором (здесь
оказывается ядерным оператором (здесь 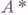 - оператор, сопряженный к 4, а
- оператор, сопряженный к 4, а 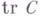 - след оператора С). Совокупность всех Г.- Ш. о. пространства Аобразует гильбертово пространство со скалярным произведением
- след оператора С). Совокупность всех Г.- Ш. о. пространства Аобразует гильбертово пространство со скалярным произведением 
Если 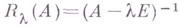 - резольвента А, а
- резольвента А, а
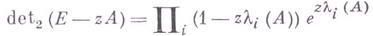
- его регуляризованный характеристический определитель, то выполнено неравенство Карлемана
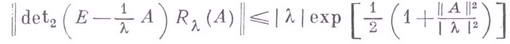 .
.
Типичный представитель Г.- Ш. о.- Гильберта - Шмидта интегральный оператор (откуда и название).
М. И. Войцеховский.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ГИЛЬБЕРТА - ШМИДТА ОПЕРАТОР" в других словарях:
Оператор Гильберта — Шмидта — это ограниченный оператор A на гильбертовом пространстве H с конечной нормой Гильберта Шмидта, т.е. для которого существует такой ортонормированный базис в H, что Если это верно в каком то ортономированном базисе, то это верно в любом… … Википедия
ГИЛЬБЕРТА - ШМИДТА ИНТЕГРАЛЬНЫЙ ОПЕРАТОР — ограниченный линейный интегральный оператор Т, действующий из пространства в и представимый в виде где ядро оператора (см. [1]). Впервые такого рода операторы рассматривались Д. Гильбертом (D. Hilbert) и Э. Шмидтом (Е. Schmidt) в 1907. Г. Ш. и. о … Математическая энциклопедия
Теорема Гильберта-Шмидта — распространяет на вполне непрерывные симметричные операторы в гильбертовом пространстве известный факт о приведении матрицы самосопряженного оператора в конечномерном евклидовом пространстве к диагональной форме в некотором ортонормированном… … Википедия
Оператор Гильберта — Шмидта это ограниченный оператор на гильбертовом пространстве с конечной нормой Гильберта Шмидта, т. е. для которого существует такой ортонормированный базис в , что Если это верно в каком то ортономированном базисе, то это верно в любом… … Википедия
Теорема Гильберта — Шмидта распространяет на вполне непрерывные симметричные операторы в гильбертовом пространстве известный факт о приведении матрицы самосопряженного оператора в конечномерном евклидовом пространстве к диагональной форме в некотором… … Википедия
ИНТЕГРАЛЬНЫЙ ОПЕРАТОР — отображение когда закон соответствия Азадается с помощью интеграла. И. о. наз. иногда интегральным преобразованием. Так, напр., для интегрального оператора Урысона (см. Урысона уравнение): закон соответствия Аопределяется интегралом (или оператор … Математическая энциклопедия
ШТУРМА - ЛИУВИЛЛЯ ОПЕРАТОР — самосопряженный оператор, порожденный дифференциальным выражением и подходящими граничными условиями в гильбертовом пространстве L2( а, b), где ( а, b) конечный или бесконечный интервал, р , р, q непрерывные действительные функции и р(х)>0 при… … Математическая энциклопедия
ИНТЕГРАЛЬНЫЙ ОПЕРАТОР — обобщение понятия матрицы на бесконечно мерный случай. Матрица Kij отображает векторы xj из векторного пространства X в векторы yi=Kijxj пространства Y. Простейший линейный И. о. определяется равенством y(t)= K(t,s)x(s)ds, и отображает ф ции… … Физическая энциклопедия
Теорема Сазонова — Эта статья содержит незавершённый перевод с иностранного языка. Вы можете помочь проекту, переведя её до конца. Если вы знаете, на каком языке написан фрагмент, укажите его в этом шаблоне. Теорема Сазонова о … Википедия
Функциональный анализ (математ.) — Функциональный анализ, часть современной математики, главной задачей которой является изучение бесконечномерных пространств и их отображений. Наиболее изучены линейные пространства и линейные отображения. Для Ф. а. характерно сочетание методов… … Большая советская энциклопедия
 в Нвыполнено условие:
в Нвыполнено условие: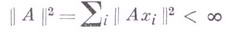
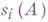 и для собственных чисел
и для собственных чисел 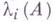 имеет место:
имеет место: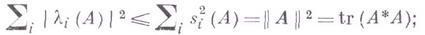
 оказывается ядерным оператором (здесь
оказывается ядерным оператором (здесь 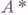 - оператор, сопряженный к 4, а
- оператор, сопряженный к 4, а 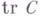 - след оператора С). Совокупность всех Г.- Ш. о. пространства Аобразует гильбертово пространство со скалярным произведением
- след оператора С). Совокупность всех Г.- Ш. о. пространства Аобразует гильбертово пространство со скалярным произведением 
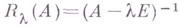 - резольвента А, а
- резольвента А, а 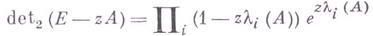
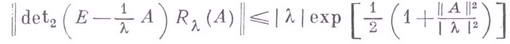 .
.