ПСЕВДОДИФФЕРЕНЦИАЛЬИЫЙ ОПЕРАТОР

оператор, действующий в функциональных пространствах на дифференцируемом многообразии и локально по определенным правилам записываемый с помощью нек-poй функции, обычно наз. символом П. о., и удовлетворяющей оценкам производных определенного типа, аналогичных оценкам производных полиномов, являющихся символами дифференциальных операторов. Пусть W - открытое подмножество в 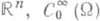- пространство бесконечно дифференцируемых функций с компактные носителем, принадлежащим W. Простейший П. о. в W - это оператор , задаваемый формулой

(1)

где - мера Лебега на - обычное скалярное произведение векторов хи - преобразование Фурье функции и, то есть

(интеграл здесь и выше берется по ), р( х,x) - гладкая функция на , удовлетворяющая нек-рым условиям и называемая символом П. о. Р. Оператор Рвида (1) обозначается также р( х, D).или р( х, D_x). Если

- многочлен от x с коэффициентами

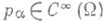
(здесь а - мультииндекс, т. е. , a_j - целые, , то р( х, D).совпадает с дифференциальным оператором, получаемым, если в выражение для р( х,x) вместо x подставить вектор

Часто используется класс символов , удовлетворяющих условиям

(2)

где a, b - мультииндексы, 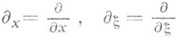, -компакт в W. Этот класс обозначается (или

Обычно предполагается, что . Через (или 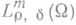) обозначается класс операторов (также называемых П. о. в W) вида р( х, D)+K, где а К - интегральный оператор с бесконечно дифференцируемым ядром, т. е. оператор вида

где 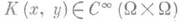. Функцию р( х,x) по-прежнему ная. символом П. о. р( х, D)+K, хотя теперь она определена уже не однозначно, а с точностью до символов, принадлежащих . Оператор 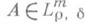наз. П. о. порядка не выше m и типа r, d. Описанный выше дифференциальный оператор принадлежит классу 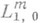. Наименьшее возможное значение тчасто ная. порядком П. о. Классы часто наз. классами Хёрмандера.

Можно задавать П. о. в Wс помощью двойных-символов, т. е. в виде

(3)

При эта формула переходит в (1). Обычно предполагается, что 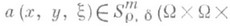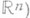, то есть

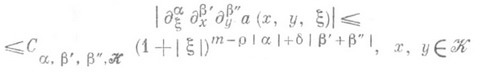(4)

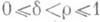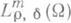где - компакт в W. Если , то построенный класс операторов вида (3) (со всевозможными функциями ) совпадает с классом . При этом символ р( х,x) (определенный с точностью до символов из 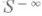) имеет следующее асимптотич. разложение:

где a!=a₁! . . . a_n! и суммирование ведется по всем мультииндексам. Эта запись означает, что разность между р( х,x) и частью суммы, взятой по тем a, для к-рых 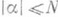, является символом, принадлежащим , т. е. символом, порядок к-рого не выше наибольшего из порядков оставшихся членов.

П. о. Р продолжается по непрерывности или с помощью двойственности до оператора 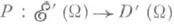, где D'(W) и - пространства обобщенных функций и обобщенных функций с компактным носителем в W соответственно. Если d<1, то при этом П. о. обладает следующим свойством псевдолокальности: если , где , то . Другая формулировка свойства псевдолокальности: ядро К( х, у )(всмысле Шварца) оператора Рбесконечно дифференцируемо по х, у при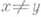

Классический П. о. порядка т. в W - П. о. , символ к-рого р( х,x) допускает асимптотич. разложение

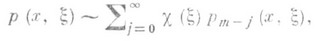
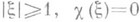где при при 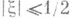, и положительно однородна по x порядка т-j

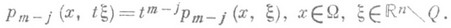
Примером классического П. о. является дифференциальный оператор (с гладкими коэффициентами). Функция р _т( х,x) наз. главным символом классического П. о.

П. о. в W наз. собственным (или П. о. с собственным носителем, или П. о. с компактным носителем), если проекции носителя его ядра при проектировании W X W на каждый сомножитель являются собственными отображениями. Собственный П. о. Ротображает в и продолжается по непрерывности до отображений 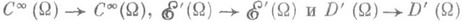, он может быть записан в виде (1) с символом р( х,x)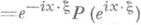, где экспонента в скобках рассматривается как функция от х, а x является параметром.

Пусть А, В- два П. о. в W, из к-рых один является собственным. Тогда имеет смысл их произведение (композиция) С=АВ. Важную роль в теории П. о. играет теорема о композиции: если ,

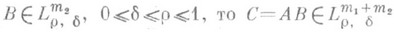. Если при этом - символы операторов С, А, В, то

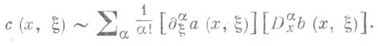
В частности, если А, В - классические П. о. порядков m₁, m₂, то С- классический П. о. порядка m₁+m₂ с главным символом 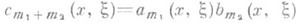, где 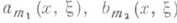- главные символы операторов Аи B.

Если , то существует и единствен сопряженный П. <о. , для к-рого скалярное произведение uи vв L₂(W). Если при этом d<r и р*( х,x) - символ II. о. Р*, а р( х,x) - символ Р, то

Таким образом, собственные П. о. при 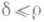образуют алгебру с инволюцией, задаваемой переходом к сопряженному оператору. Произвольные П. о. образуют модуль над этой алгеброй.

Теорема об ограниченности П. о. классов Хёрмандера в L₂ -нормах в наиболее точной форме состоит в следующем (см. [8]): пусть , оператор Римеет вид (3) с двойным символом а( х, у,x), удовлетворяющим оценкам (4), где числа т,r, d удовлетворяют условиям

(5)

тогда оператор Рпродолжается до ограниченного оператора . В частности, при условии (5) ограничены в 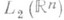П. о. вида (1) с символами, удовлетворяющими оценкам (2) равномерно по х (т. е. с постоянными , не зависящими от ). Отсюда следует, напр., ограниченность в операторов , если и ядро оператора Римеет компактный носитель (или оценки символа опять-таки равномерны по х). При r<d или при d=1 операторы такого вида уже не обязательно ограничены. Аналогично, в общей ситуации невыполнение одного из двух последних условий (5) уже дает класс П. о., содержащий неограниченные операторы.

В терминах оценок символа можно дать условия ограниченности П. о. в L_p -нормах, а также в гёльдеровых и в жевреевских нормах (см. [8]).

Если в Rⁿ дан оператор Р=р( х, D), где 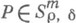, , 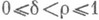причем оценки (2) равномерны по , то этот оператор продолжается до ограниченного оператора

где означает

обычное пространство Соболева на (иногда обозначаемое также .

Класс П. о. при в естественном смысле инвариантен относительно диффеоморфизмов так же, как и его подкласс классических П. о. Это позволяет определить класс П. о. 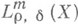и классические П. о. на произвольном гладком многообразии X. Формула замены переменной в символе при диффеоморфизме 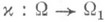, где W, W₁ - области в X, имеет вид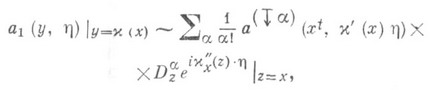

где а( х,x) - символ оператора 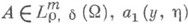- символ оператора 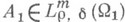, заданного формулой , т. е. полученного из Азаменой переменных 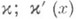обозначает якобиан отображения - транспонированная матрица,

В частности, отсюда следует, что главный символ классического П. о. на многообразии Xявляется корректно определенной функцией на кокасательном расслоении Т*Х.

Если X - компактное многообразие (без края), то П. о. на Xобразуют алгебру с инволюцией, если вводить инволюцию с помощью скалярного произведения, задаваемого гладкой положительной плотностью. Оператор ограничен в L₂(X), а если А , где m<0, то такой П. о. компактен в L₂(X). Для классических П. о. Апорядка 0 на X

где а ₀( х,x) - главный символ оператора А, а K пробегает множество всех компактных операторов в L₂(X). Оператор 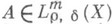непрерывно отображает H^s(X).в H^s-m(X).при любом .

Параметриксом П. о. Аназ. такой П. о. В, что I-AB и I-ВA - П. о. порядка 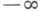, т. е. интегральные операторы с гладким ядром. Пусть , - символ оператора А. Достаточным условием существования параметрикса оператора Аявляется выполнение оценок:

(6)

В этом случае существует параметрикс Простейшим следствием существования параметрикса является гипоэллиптичность оператора А:если А 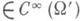, где , то 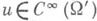. Иными словами, sing supp Au=sing supp и. Верен также следующий более точный факт (теорема регулярности): если 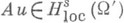, то . Имеет место и микролокальная теорема регулярности: WF(Au)=WF(u), где WF(u).означает волновой фронт обобщенной функции u.

Условия (6) при 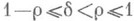инвариантны относительно диффеоморфизмов. Поэтому имеет смысл соответствующий класс операторов на многообразии X. Если X - компактное многообразие, то такой оператор Афредгольмов в , т. е. имеет в 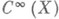конечномерные ядро и коядро, а также замкнутый образ.

Классический П. о. Апорядка m с главным символом а _т( х,x) наз. эллиптическим, если при 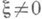. Такой оператор удовлетворяет условиям (6) с m₀=m и имеет параметрикс, также являющийся классическим П. о. порядка - m. На компактном многообразии Xтакой П. о. задает фредгольмов оператор

Все эти определения и факты переносятся на П. о., действующие в вектор-функциях или, более общо, в сечениях векторных расслоений. Для эллиптич. оператора на компактном многообразии Xиндекс задаваемого им отображения на соболевских классах сечений не зависит от и может быть явно вычислен (см. Индекса формулы).

Роль П. о. состоит в том, что имеется ряд операций, выводящих за класс дифференциальных операторов, но сохраняющих класс П. о. Напр., резольвента и комплексные степени эллиптического дифференциального оператора на компактном многообразии являются классическими П. о., они возникают при сведении на границу эллиптической граничной задачи (см., напр., [7], [8] и предпоследнюю статью в [1]).

Существуют разные варианты теории П. о., приспособленные к решению различных задач анализа и ма-тематич. физики. Часто возникают П. о. с параметром, необходимые, напр., для изучения резольвенты и асимптотики собственных значений. Важную роль играют различные варианты теории П. о. на Rⁿ, учитывающие эффекты, связанные с описанием поведения функции на бесконечности, и частично инспирированные математич. вопросами квантовой механики, возникающими при изучении квантования классич. систем (см. [5], [1]). В теории локальной разрешимости уравнений с частными производными и в спектральной теории полезны П. о., поведение к-рых описывается с помощью весовых функций, заменяющих |x| в оценках типа (2) (см. [8], [14]). Построена алгебра П. о. на многообразии с краем, содержащая, в частности, параметрикс эллиптической граничной задачи (см. [3], [13]).

Частным случаем П. о. являются многомерные сингулярные интегральные и интегро-дифференциальные операторы, изучение которых подготовило появление теории П. о. (см. [10]).

Теория П. о. служит основой для изучения интегральных операторов Фурье (см. [7], [10]), играющих ту же роль в теории гиперболич. уравнений, что и П. о. в теории эллиптич. уравнений.

Лит.:[1] Псевдодифференциальные операторы, пер. с англ., М., 1967; [2] Агранович М. С., Вишик М. И., Псевдодифференциальные операторы, М., 1968; [3]Эскин Г. И., Краевые задачи для эллиптических псевдодифференциальных уравнений, М., 1973; [4] Грушин В. В., Псевдодифференциальные операторы, М., 1975; [5] Жубин М. А., Псевдодифференциальные операторы и спектральная теория, М., 1978; [6] Priedrichs К. О., Pseudo-differential operators, N. Y., 1970; [7] Treves F., Introduction to pseudo-differential and Fourier integral operators, v. 1-2, N. Y., 1980; [8] Тay1оr М., Pseudo-differential operators, В.- [u. a.], 1974; [9] Kumano-go H., Pseudo-differential operators, Camb., 1981; [10] Duistermaat J., Fourier integral operators, N. Y., 1973; [11] Маслов В. П., Федорюк М. В., Квазиклассическое приближение для уравнений квантовой механики, М., 1976; [12] Агранович М. С., "Успехи матем. наук", 1965, т. 20, в. 5, с. 3-120; [13] Boutet de MonvelL., "Acta math.", 1971, v. 126, p. 11-51; [14] HormanderL., "Comm. Pure Appl. Math.", 1979, v. 32, Mi 3,p. 359-443.

М. А. Шубин.