Внутренний автоморфизм — Aвтоморфизм модели изоморфизм, отображающий модель на себя. Совокупность всех автоморфизмов некоторой модели с операцией композиции и тождественным отображением в качестве нейтрального элемента образует группу. Группа автоморфизмов модели K… … Википедия
АЛГЕБРАИЧЕСКОЙ СИСТЕМЫ АВТОМОРФИЗМ — Ч изоморфное отображение алгебраической системы на себя. Автоморфизмом (А.) системы наз. всякое взаимно однозначное отображение множества Ана себя, обладающее свойствами: для всех . из Аи для всех из . Другими словами, А … Математическая энциклопедия
МОДУЛЬ АВТОМОРФИЗМА — действительное положительное число, ставящееся в соответствие автоморфизму локально компактной группы. Если G такая группа и нек рый автоморфизм группы Gкак топологич. группы, то модуль автоморфизма определяется формулой где левоинвариантная мера … Математическая энциклопедия
СОВЕРШЕННАЯ ГРУППА — группа . такая, что ее центр есть единичная подгруппа (т. е. G т. н. группа без центра) и любой ее автоморфизм является внутренним (см. Внутренний автоморфизм). Группа автоморфизмов С. г. G изоморфна самой группе . (с чем и связан термин… … Математическая энциклопедия
ЭРГОДИЧЕСКАЯ ТЕОРИЯ НЕКОММУТАТИВНАЯ — раздел теории операторных алгебр, изучающий автоморфизмы С* алгебр с точки зрения эргодической теории. Круг вопросов, рассматриваемых в Э. т. н., и полученные (к 1984) результаты можно в основном разделить на три группы. К первой группе относятся … Математическая энциклопедия
Модуль автоморфизма — Связать? Модуль автоморфизма вещественное положительное число, ставящееся в соответствие автоморфизму, локально компактной группы. Если такая группа и … Википедия
Унимодулярная группа — Модуль автоморфизма вещественное положительное число, ставящееся в соответствие автоморфизму, локально компактной группы. Если G такая группа и A некоторый автоморфизм группы G как топологической группы, то модуль автоморфизма а определяется… … Википедия
ЛИ ГРУППА — группа G, обладающая такой структурой аналитического многообразия, что отображение прямого произведения в Gана литично. Другими словами, Ли г. это множество, наделенное согласованными структурами группы и аналитич. многообразия. Ли г. наз.… … Математическая энциклопедия
НЕАБЕЛЕВЫ КОГОМОЛОГИИ — когомологии со значениями в неабелевой группе, пучке неабелевых групп и т. д. Наиболее известные примеры Н. к. это когомологии групп, топологич. пространств и, более обще, топологизированных категорий в размерностях 0, 1. Единый подход к Н. к.… … Математическая энциклопедия
ФУНДАМЕНТАЛЬНАЯ ГРУППА — группа Пуанкаре, первая абсолютная гомотопическая группа Пусть / отрезок [0, 1], его граница. Элементами Ф. г. пунктированного топологич. пространства (X, х0 )служат гомотопич. классы замкнутых путей в X, т. е. классы гомотопных rel {0, 1}… … Математическая энциклопедия
 такой, что
такой, что 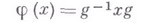
 . Совокупность всех В. а. группы Gобразует нормальную подгруппу в группе всех автоморфизмов G, эта подгруппа изоморфна
. Совокупность всех В. а. группы Gобразует нормальную подгруппу в группе всех автоморфизмов G, эта подгруппа изоморфна  , где
, где  - центр группы G. Автоморфизмы, не являющиеся внутренними, наз. внешними.
- центр группы G. Автоморфизмы, не являющиеся внутренними, наз. внешними.