НЕАБЕЛЕВЫ КОГОМОЛОГИИ

- когомологии со значениями в неабелевой группе, пучке неабелевых групп и т. д. Наиболее известные примеры Н. к.- это когомологии групп, топологич. пространств и, более обще, топологизированных категорий в размерностях 0, 1. Единый подход к Н. к. дает следующее понятие. Пусть - группы,- множество с отмеченной точкой е, Aff С ¹-. голоморф группы - группа преобразований множества , сохраняющих е. Тогда неабелев коцепной комплекс - это набор где - гомоморфизмы, а - такое отображение, что

Определяются 0-мерная группа когомологии

и 1-мерное множество (с отмеченной точкой) когомологии где а факторизация проводится при помощи действия r группы

Примеры. 1) Пусть X- топологич. пространство с пучком групп - его покрытие; тогда имеется комплекс Чеха

где определяются так же, как в абелевом случае (см. Когомологии),

Когомологии при переходе к пределу по покрытиям дают когомологии пространства Xсо значениями в 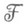. При этом.. Если - пучок ростков непрерывных отображений со значениями в топопогич. группе G, то ,интерпретируется как множество классов изоморфных топологических главных расслоений над X со структурной группой G. В аналогичных терминах получается классификация гладких и голоморфных главных расслоений. Таким же способом определяются Н. к. топологизированной категории; по поводу их интерпретации см. Главный G-объект.

2) Пусть G - нек-рая группа и А- (не обязательно абелева) G-группа, т. е. операторная группа с группой операторов G. Пусть результат действия оператора на элемент обозначается . Комплекс определяется формулами:

Группа совпадает с подгруппой А ^G неподвижных точек в Аотносительно G, а множество 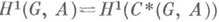есть множество классов эквивалентных скрещенных гомоморфизмов и интерпретируется как множество классов изоморфных главных однородных пространств над А. По поводу приложений и конкретных вычислений Н. к. групп см. Галуа когомологии. Аналогично определяются Н. к. категорий и полугрупп.

3) Пусть X - гладкое многообразие, G- группа Ли,- ее алгебра Ли. Неабелев комплекс д е Рама определяется следующим образом: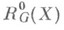

- группа всех гладких функций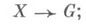

-пространство внешних k-формна Xсо значениями в g.

Множество есть множество классов вполне интегрируемых уравнений вида относительно калибровочных преобразований. Аналог теоремы де Рама дает интерпретацию этого множества как нек-рого подмножества в множестве классов сопряженных гомоморфизмов

В случае комплексного многообразия М и комплексной группы Ли Gопределяются также неабелевы голоморфный комплекс де Рама и комплекс Дольбо, тесно связанные с задачей классификации голоморфных расслоений [3]. Неабелевы комплексы дифференциальных форм являются также важным аппаратом в теории псевдогрупповых структур на многообразиях [7].

С каждым подкомплексом неабелева коцепного комплекса связана точная последовательность когомоло-гип. Напр., для комплекса C*(G, А )из примера 2) и его подкомплекса C*(G, В), где Весть G-инвариаитная подгруппа в А, она имеет вид

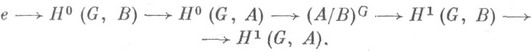
Если В- нормальный делитель в А, то последовательность можно продолжить до члена а если Влежит в центре, то - и до . Эта последовательность точна в категории множеств с отмеченными точками. Кроме того, существует аппарат ("подкручивание" или "скручивание" коцепного комплекса), позволяющий описывать прообразы всех, а не только отмеченных элементов (см. [1], [6], [3]). Можно построить также спектральную последовательность, связанную с двойным неабелевым комплексом, и соответствующую краевую точную последовательность [4].

Кроме описанных выше 0-мерных и 1-мерных, существуют также 2-мерные Н. к. Классич. примером являются 2-мерные когомологии группы Gсо значениями в нек-рой группе А, к-рые определяются следующим образом. Через обозначается множество всех пар , где 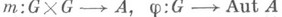- такие отображения, что

здесь Int a- внутренний автоморфизм, порожденный элементом 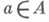. В определяется отношение эквивалентности: , если существует такое отображение , что

и

Классы этой эквивалентности и составляют множество когомологии ,. Они находятся во взаимно однозначном соответствии с классами эквивалентных расширений группы Апри помощи G(см. Расширение группы).

Соответствие дает отображение множества в множество всех гомоморфизмов

пусть для . Если фиксировать , то на центре группы Абудет задана структура G-модуля и тем самым определены группы когомологии . Оказывается, что непустота множества равносильна тривиальности нек-рого класса из . Далее, при этом условии группа просто транзитивно действует на множестве .

Это определение двумерных когомологии можно обобщить, перенеся его на топологизированные категории (см. [2], где даны также приложения этого понятия). Общая алгебраич. схема, приводящая к двумерным когомологиям, указана в [4]; так же, как и в описанном выше частном случае, их вычисление сводится к вычислению одномерных неабелевых и обычных абелевых когомологии.

Лит.:[1] Серр Ж.-П., Когомологии Галуа, пер. с франц., М., 1968; [2] Giraud J., Cohomologie non abelienne, В.- Hdlb.- N. Y., 1971; [3] Онищик А. Л., "Тр. Моск. матем. об-ва", 1967, т. 17,с. 45-88; [4]Толпыго А. К., в сб.: Вопросы теории групп и гомологической алгебры, в. 1, Ярославль, 1977, с. 158-97; [5] Dedecker Р., в кн.: Category theory, homology theory and their applications, v. 2, B.- Hdlb.- N. Y.. 1969, p. 32-64; [6] Frenkel J., "Bull. Soc. math. France", 1957, t. 85, № 2, p. 135-220; [7] Goldschmidt H., "Bull. Amer. Math. Soc", 1978, v. 84, № 4, p. 531-46; [8] Springer Т. А., в кн.: Proceudings of Symposia in pure mathematics, Providence, v. 9, 1966, p. 164-82.

A. Л. Онищик, А. К. Толпыго