ВНУТРЕННИЙ ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР
- ВНУТРЕННИЙ ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР
относительно поверхности  - дифференциальный оператор L(u), обладающий тем свойством, что для любой функции, для к-рой он определен, его значение в точке
- дифференциальный оператор L(u), обладающий тем свойством, что для любой функции, для к-рой он определен, его значение в точке 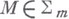 может быть вычислено лишь по значениям этой функции на ы адкой поверхности
может быть вычислено лишь по значениям этой функции на ы адкой поверхности 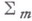 , заданной в пространстве
, заданной в пространстве  В. д. о. может быть вычислен с помощью производных в направлениях l, к-рые лежат в касательном к поверхности
В. д. о. может быть вычислен с помощью производных в направлениях l, к-рые лежат в касательном к поверхности  многообразии. Если ввести такие координаты, что на
многообразии. Если ввести такие координаты, что на  :
:
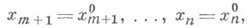
то оператор  , если он внутренний относительно
, если он внутренний относительно  , после надлежащих преобразований не будет содержать производных по переменным
, после надлежащих преобразований не будет содержать производных по переменным  (так наз. выводящих производных). Напр., оператор
(так наз. выводящих производных). Напр., оператор
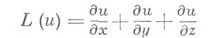
есть В. д. о. относительно любой гладкой поверхности, составленной из прямых  а также относительно любой из этих прямых. Если оператор
а также относительно любой из этих прямых. Если оператор 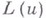 является В. д. о. относительно поверхности
является В. д. о. относительно поверхности  то
то 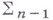 наз. характеристикой дифференциального уравнения
наз. характеристикой дифференциального уравнения 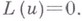
Иногда оператор наз. внутренним по отношению к поверхности  если в точках этой поверхности старший порядок выводящих производных ниже порядка оператора. Б. Л. Рождественский.
если в точках этой поверхности старший порядок выводящих производных ниже порядка оператора. Б. Л. Рождественский.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ВНУТРЕННИЙ ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР" в других словарях:
Интегро-дифференциальные уравнения — Интегро дифференциальные уравнения класс уравнений, в которых неизвестная функция содержится как под знаком интеграла, так и под знаком дифференциала. где называется внешним дифференциальным оператором, а … Википедия
СИМВОЛ ОПЕРАТОРА — скалярная или матричная функция, ассоциированная с оператором и обладающая свойствами, в той или иной форме отражающими свойства этого оператора. Обычно считается, что С. о. заданы для операторов, принадлежащих нек рой алгебре. Тогда, как правило … Математическая энциклопедия
Список операторов — Данный список содержит математические преобразования, кроме интегральных преобразований. Выражение Задание кривой Переменные Описание Линейные преобразования Производная n го порядка Декартовы координаты Интеграл, площадь … Википедия
Условный — 7. Условный Содержащееся в справочнике сообщений или сегментов условие необязательного использования сегмента, элемента данных, составного элемента данных или компонентного элемента данных Источник: ГОСТ 6.20.1 90: Электронный обмен данными в… … Словарь-справочник терминов нормативно-технической документации
Манн, Майкл — (Mann, Michael) Режиссер, сценарист, оператор, продюсер, актер. Родился 5 февраля 1943 года в Чикаго. Получил образование в Висконсинском университете. Окончил также Лондонскую киношколу. Подобно многим другим режиссерам своего поколения,… … Режиссерская энциклопедия. Кино США
 - дифференциальный оператор L(u), обладающий тем свойством, что для любой функции, для к-рой он определен, его значение в точке
- дифференциальный оператор L(u), обладающий тем свойством, что для любой функции, для к-рой он определен, его значение в точке 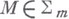 может быть вычислено лишь по значениям этой функции на ы адкой поверхности
может быть вычислено лишь по значениям этой функции на ы адкой поверхности 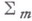 , заданной в пространстве
, заданной в пространстве  В. д. о. может быть вычислен с помощью производных в направлениях l, к-рые лежат в касательном к поверхности
В. д. о. может быть вычислен с помощью производных в направлениях l, к-рые лежат в касательном к поверхности  многообразии. Если ввести такие координаты, что на
многообразии. Если ввести такие координаты, что на  :
: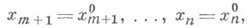
 , если он внутренний относительно
, если он внутренний относительно  , после надлежащих преобразований не будет содержать производных по переменным
, после надлежащих преобразований не будет содержать производных по переменным  (так наз. выводящих производных). Напр., оператор
(так наз. выводящих производных). Напр., оператор 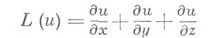
 а также относительно любой из этих прямых. Если оператор
а также относительно любой из этих прямых. Если оператор 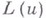 является В. д. о. относительно поверхности
является В. д. о. относительно поверхности  то
то 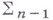 наз. характеристикой дифференциального уравнения
наз. характеристикой дифференциального уравнения 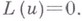
 если в точках этой поверхности старший порядок выводящих производных ниже порядка оператора. Б. Л. Рождественский.
если в точках этой поверхности старший порядок выводящих производных ниже порядка оператора. Б. Л. Рождественский.