Фундаментальная область — Фундаментальной областью группы движений называется такое множество точек пространства, что для любой точки пространства есть ровно одна точка её орбиты в … Википедия
Область (математика) — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Фундаментальная наука — Запрос «Фундаментальные исследования» перенаправляется сюда; см. также другие значения. Фундаментальная наука область познания, подразумевающая теоретические и экспериментальные научные исследования основополагающих явлений (в том числе и… … Википедия
БЕСКОНЕЧНОСВЯЗНАЯ ОБЛАСТЬ — область бесконечной связности, область, у к рой фундаментальная группа не является конечнопо рожденной. Понятие Б … Математическая энциклопедия
Многосвязная область — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
МНОГОСВЯЗНАЯ ОБЛАСТЬ — линейно связного пространства область D, в к рой существуют замкнутые пути, не гомотопные нулю, или, иначе говоря, фундаментальная группа к рой не тривиальна. Это означает, что в Dсуществуют замкнутые пути, к рые нельзя непрерывно деформировать в … Математическая энциклопедия
ОДНОСВЯЗНАЯ ОБЛАСТЬ — линейно связного пространства область D, в к рой все замкнутые пути гомотопны нулю или, иначе говоря, фундаментальная группа к рой тривиальна. Это означает, что любой замкнутый путь в Dможно непрерывно деформировать в точку, оставаясь все время в … Математическая энциклопедия
ДИСКРЕТНАЯ ГРУППА — преобразований группа Г гомеоморфизмов хаусдорфова топологич. пространства X, удовлетворяющая следующему условию: для любых точек х, найдутся такие их окрестно сти U, V соответственно, что множество конечно. Стабилизатор точки относительно Д. г.… … Математическая энциклопедия
КВАДРАТИЧНЫХ ФОРМ ПРИВЕДЕНИЕ — выделение в каждом классе квадратичных форм (к. ф.)над данным кольцом Rприведенных форм стандартных форм класса (одной или нескольких). Основной целью К. ф. п. является решение проблемы эквивалентности к. ф.: установить, эквивалентны над Rданные… … Математическая энциклопедия
Модулярная группа — Модулярная группа группа всех преобразований Мёбиуса вида … Википедия
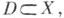 содержащее элементы из всех орбит группы Г, причем из орбит общего положения - ровно по одному элементу. Имеются различные варианты точного определения Ф. о. Иногда Ф. о. наз. любое подмножество, принадлежащее заданной s-алгебре (напр., борелевское) и содержащее по одному представителю из каждой орбиты. Однако если X - топологич. многообразие, то Ф. о. обычно наз. подмножество
содержащее элементы из всех орбит группы Г, причем из орбит общего положения - ровно по одному элементу. Имеются различные варианты точного определения Ф. о. Иногда Ф. о. наз. любое подмножество, принадлежащее заданной s-алгебре (напр., борелевское) и содержащее по одному представителю из каждой орбиты. Однако если X - топологич. многообразие, то Ф. о. обычно наз. подмножество 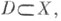 являющееся замыканием открытого подмножества и такое, что подмножества
являющееся замыканием открытого подмножества и такое, что подмножества 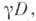
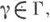 не имеют попарно общих внутренних точек и образуют локально конечное покрытие пространства X. Напр., в качестве Ф. о. группы параллельных переносов плоскости
не имеют попарно общих внутренних точек и образуют локально конечное покрытие пространства X. Напр., в качестве Ф. о. группы параллельных переносов плоскости 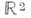 на целочисленные векторы может быть взят квадрат
на целочисленные векторы может быть взят квадрат