ФУНДАМЕНТАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
- ФУНДАМЕНТАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
последовательность Кош и, точек метрического пространства X- последовательность  п=1, 2, ... такая, что для любого
п=1, 2, ... такая, что для любого  существует такой номер п 0,что для всех номеров .> n0 и т> п 0 выполняется неравенство
существует такой номер п 0,что для всех номеров .> n0 и т> п 0 выполняется неравенство 
Обобщением Ф. п. является понятие направленности Коши в равномерном пространстве. Пусть X - равномерное пространство с равномерностью  Направленность
Направленность  -направленное множество, наз. направленностью Коши, если для каждого элемента
-направленное множество, наз. направленностью Коши, если для каждого элемента  существует такой индекс
существует такой индекс  что для всех
что для всех  и
и  следующих в Аза
следующих в Аза 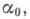 имеет место включение
имеет место включение 
Лит.:[1] Александров П. С., Введение в теорию множеств и общую топологию, М., 1977; [2] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 5 изд., М., 1981; [3] Келли Дж., Общая топология, пер. с англ., 2 изд., М., 1981,
Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "ФУНДАМЕНТАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ" в других словарях:
Фундаментальная последовательность — Фундаментальная последовательность, или сходящаяся в себе последовательность, или последовательность Коши последовательность точек метрического пространства такая, что для любого заданного расстояния существует элемент последовательности, начиная … Википедия
Последовательность Коши — Последовательность точек метрического пространства с метрикой ρ называется фундаментальной (ρ фундаментальной) или последовательностью Коши, если она удовлетворяет критерию Коши: Для любого существует такое натуральное , что … Википедия
Числовая последовательность — Последовательность Числовая последовательность это последовательность элементов числового пространства. Числовые пос … Википедия
КОШИ ПОСЛЕДОВАТЕЛЬНОСТЬ — то же, что фундаментальная последовательность … Математическая энциклопедия
Пополнение — Последовательность точек метрического пространства с метрикой ρ называется фундаментальной (ρ фундаментальной) или последовательностью Коши, если она удовлетворяет критерию Коши: Для любого существует такое натуральное , что … Википедия
Пополнение метрического пространства — Последовательность точек метрического пространства с метрикой ρ называется фундаментальной (ρ фундаментальной) или последовательностью Коши, если она удовлетворяет критерию Коши: Для любого существует такое натуральное , что … Википедия
Условие Коши — Последовательность точек метрического пространства с метрикой ρ называется фундаментальной (ρ фундаментальной) или последовательностью Коши, если она удовлетворяет критерию Коши: Для любого существует такое натуральное , что … Википедия
ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО — вещественное число, положительное число, отрицательное число или нуль. Понятие Д. ч. возникло путем расширения понятия рационального числа. Необходимость этого расширения обусловлена как практическим использованием математики при выражении… … Математическая энциклопедия
Конструктивные способы определения вещественного числа — При конструктивном подходе к определению вещественного числа вещественные числа строят, исходя из рациональных, которые считают заданными. Во всех трёх нижеизложенных способах за основу берутся рациональные числа и конструируются новые объекты,… … Википедия
МЕТРИЧЕСКОЕ ПРОСТРАНСТВО — множество Xвместе с нек рой метрикойr на ном. Теоретико множественный подход к изучению фигур (пространств) основан на исследовании взаимного расположения составляющих их элементарных частей. Одной из фундаментальных характеристик взаимного… … Математическая энциклопедия
 п=1, 2, ... такая, что для любого
п=1, 2, ... такая, что для любого  существует такой номер п 0,что для всех номеров .> n0 и т> п 0 выполняется неравенство
существует такой номер п 0,что для всех номеров .> n0 и т> п 0 выполняется неравенство 
 Направленность
Направленность  -направленное множество, наз. направленностью Коши, если для каждого элемента
-направленное множество, наз. направленностью Коши, если для каждого элемента  существует такой индекс
существует такой индекс  что для всех
что для всех  и
и  следующих в Аза
следующих в Аза 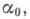 имеет место включение
имеет место включение 
