МОДУЛЬ — абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… … Математическая энциклопедия
НЕПРИВОДИМЫЙ МОДУЛЬ — простой модуль, ненулевой унитарный модуль Мнад кольцом Д с единицей, содержащий лишь два подмодуля нулевой и сам М. Примеры: 1) если кольцо целых чисел, то неприводимые R модули это абелевы группы простого порядка; 2) если R тело, то… … Математическая энциклопедия
БИЛИНЕЙНАЯ ФОРМА — на произведении модулей билинейное отображение левый унитарный модуль, W правый унитарный А модуль, А кольцо с единицей, рассматриваемое также как ( А, А ) бимодуль. Если V= W, то говорят, что f есть Б. ф. на модуле V, а также, что Vнаделен… … Математическая энциклопедия
ВЕКТОРНОЕ ПРОСТРАНСТВО — линейное пространство, над полем К, аддитивно записанная абелева группа Е, в которой определено умножение элементов на скаляры, т. е. отображение удовлетворяющее следующим аксиомам Из аксиом 1) 4) вытекают следующие важные свойства векторного… … Математическая энциклопедия
ПОЛИНОМИАЛЬНАЯ ФУНКЦИЯ — обобщение понятия целой рациональной функции (см. Многочлен). Пусть V унитарный модуль над ассоциативно коммутативным кольцом С с единицей. Отображение j: наз. П. ф., если j=j0+...+jm, где ji форма степени iна V, i=0,1,...,т(см. Полилинейная… … Математическая энциклопедия
СИММЕТРИЧЕСКАЯ АЛГЕБРА — обобщение алгебры многочленов. Если М унитарный модуль над коммутативно ассоциативным кольцом Ас единицей, то С. а. модуля Мназ. алгебра S(M)=T(M)/I, где Т(М) тензорная алгебра модуля М, I ее идеал, порожденный элементами вида . С. а.… … Математическая энциклопедия
Макрушин, Андрей Валентинович — Андрей Валентинович Макрушин Дата рождения: 15 июля 1934( … Википедия
КВАДРАТИЧНАЯ ФОРМА — над коммутативным люльцом с единицей однородный многочлен от n=n(q)переменных с коэффициентами Обычно R это поле С, R или Q, либо кольцо Z, кольцо целых элементов алгебраич. числового поля, а также их пополнения по неархимедовым нормам.… … Математическая энциклопедия
Алгебра Ли — Алгебра Ли объект абстрактной алгебры. Естественно появляется при изучении инфинитезимальных свойств групп Ли. Названа по имени норвежского математика Софуса Ли (1842 1899). Содержание 1 Определение 1.1 Замечания … Википедия
ЛИ АЛГЕБРА — лиева алгебра, унитарный k модуль Lнад коммутативным кольцом k с единицей, к рый снабжен билинейным отображением прямого произведения в L, обладающим следующими двумя свойствами: 1) [ х, х] = 0 (откуда вытекает антикоммутативность 2) ( х,[ у,… … Математическая энциклопедия
 (соответственно
(соответственно  для правого модуля),
для правого модуля), 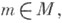 - тождественный автоморфизм группы М.
- тождественный автоморфизм группы М. 