- ТРИКОМИ ЗАДАЧА
- - задача отыскания решения уравнения смешанного эллиптико-гиперболического типа с двумя независимыми переменными и с одной гладкой разомкнутой линией параболического вырождения АВ, принимающего заданные значения на эллиптической части
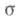 границы
границы  области
области  задания уравнения и на одной из двух характеристик АС или ВС, образующих гиперболическую часть
задания уравнения и на одной из двух характеристик АС или ВС, образующих гиперболическую часть  границы
границы  (см. Смешанного типа уравнение). Т. з. для Трикоми уравнения
(см. Смешанного типа уравнение). Т. з. для Трикоми уравнения 
в области
 ограниченной гладкой кривой
ограниченной гладкой кривой 
 с концами в точках А(0, 0), В(1,0) и характеристиками АС и ВС:
с концами в точках А(0, 0), В(1,0) и характеристиками АС и ВС: 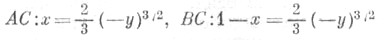
впервые была поставлена и изучена Ф. Трикоми (F. Tricomi, [1], [2]).
При определенных ограничениях на гладкость заданных функций и характер поведения производной uy искомого решения ив точках Аи ВТ. з.:
Для уравнения (1) редуцируется к отысканию регулярного в области
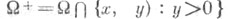 решения и=и( х, у )уравнения (1), удовлетворяющего краевым условиям
решения и=и( х, у )уравнения (1), удовлетворяющего краевым условиям 
где - однозначно определяется через
- однозначно определяется через  - оператор дробного (в смысле Римана - Лиувилля) дифференцирования порядка 2/3:
- оператор дробного (в смысле Римана - Лиувилля) дифференцирования порядка 2/3: 
Г (z) - гамма-функция Эйлера.
Решение задачи (1), (3) в свою очередь сводится к нахождению функции v(х)=и у(x,0) из нек-рого сингулярного интегрального уравнения. Это уравнение в случае, когда совпадает с нормальным контуром
совпадает с нормальным контуром 
имеет вид

где f(x) явно выражается через и
и  а интеграл понимается в смысле глазного значения по Коши (см. [1] - [4]).
а интеграл понимается в смысле глазного значения по Коши (см. [1] - [4]).
При доказательство единственности и существования решения Т. з. наряду с принципом экстремума Бицадзе (см. Смешанного типа уравнение )и методом интегральных уравнений широко используется так наз. метод а b с, сущность к-рого заключается в том, что для данного дифференциального оператора 2-го порядка L(напр., Т) с областью определения D(L)строится дифференциальный оператор 1-го порядка
обладающий тем свойством, что
где C=const>0;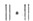 -нек-рая норма (см. [5]).
-нек-рая норма (см. [5]).
Т. з. получила обобщения как на случай уравнений смешанного типа с несколькими линиями параболиче-
ского вырождения (см. [6]) так и на случай уравнений смешанного гиперболо-параболического типа (см. [7]).Лит.:[1] Трикоми Ф., О лилейных уравнениях в частных производных второго порядка смешанного типа, пер. с итал., М.- Л., 1947; [2] его жe, Лекции по уравнениям в частных производных, пер. с итал., М., 1957; [3] Бицадзе А. В., К проблеме уравнений смешанного типа, М., 1953: [4] его же, Уравнения смешанного типа, М., 1959; [5] Берс Л., Математические вопросы дозвуковой и околозвуковой газовой динамики, пер. с англ., М., 1961; [6] Нахушев А. М., лДокл. АН СССР
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
