ГЕЛЛЕРСТЕДТА ЗАДАЧА

- краевая задача для уравнения типа Чаплыгина вида

в к-ром функция возрастает, при . Искомая функция задается на границе, состоящей из достаточно гладкого контура и кусков характеристик. Рассматриваемое уравнение эллиптично в полуплоскости , параболично на линии у=0 и гиперболично при . Гиперболич. полуплоскость покрывается двумя семействами характеристик, удовлетворяющих уравнениям

.

На линии характеристики одного семейства переходят в характеристики другого семейства.

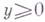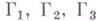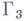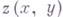Пусть Е - односвязна'я область с границей, состоящей из достаточно гладкого контура Г при и из кусков характеристик и при , причем , - характеристики одного семейства, а - другого (см. рис.). В Есправедлива теорема существования и единственности решений следующих краевых задач: функция задается на функция задается на

Впервые эти задачи были изучены (для К(y)= 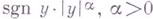) С. Геллерстедтом [1] методами, развитыми Ф. Трикоми [2] для Трикоми задачи, и представляют собой обобщение последней. Г. з. имеют важные приложения в околозвуковой газовой динамике. Г. з. и родственные им задачи исследовались для нек-рых многосвязных областей и для линейных уравнений, содержащих младшие члены (см. [3]).

Лит.:[l] Gellerstedt S., "Arkiv for mat., astr. och fysik", 1938, Bd 26A, № 3, p. 1-32; [2] Трикоми Ф., Лекции по уравнениям в частных производных, пер. с итал., М., 1957; [3] Смирнов М. М. Уравнения смешанного типа, М., 1970. Л. П. Купцов.