КОШИ ХАРАКТЕРИСТИЧЕСКАЯ ЗАДАЧА

- задача отыскания решения дифференциальных уравнений или систем уравнений с частными производными по заданным его значениям на характеристических многообразиях.

Для широкого класса уравнений гиперболического и параболического типов в пространстве E_n+1 независимых переменных носителями данных могут служить определенным образом ориентированные незамкнутые n-мерные поверхности S. Если, напр., Sявляется поверхностью пространственного типа, то Коши задача (с начальными данными на S).поставлена всегда корректно. В К. х. з. носителем данных является исключительно характеристическое многообразие (или ее определенная часть). В этом случае задача Коши может и вовсе не иметь решения, а если и имеет таковое, то оно может быть неединственным.

Напр., К. х. з. для уравнения (n=1, х ₁=х) с данными на характеристике t=0 некорректна. Если решение К. х. з. существует, то из уравнения и из второго начального условия вытекает необходимое условие ее разрешимости: 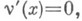то есть решение К. х. з. может существовать лишь при В этом случае, если решение действительно существует и задается формулой где - любая функция класса С ², удовлетворяющая условиям

Для существования решения К. х. з. для линейных систем гиперболических уравнений требуется, чтобы ранг расширенной матрицы системы был равен вдоль характеристической поверхности Sрангу вырожденной матрицы.

Существует широкий класс гиперболических уравнений и систем, для к-рых в качестве носителя данных могут служить характеристические поверхности. Так, напр., для уравнения

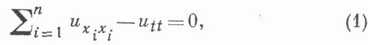
когда характеристическая поверхность Sпредставляет собой конус

К. х. з. ставится так: найти регулярное внутри конуса (2) решение и( х, t).уравнения (1), принимающее на конусе (2) наперед заданные значения.

В случае пространственного переменного(n=1, х ₁=х).конус (2) представляет собой пару прямых , проходящих через точку ( х ₀, t₀). Эти прямые разбивают плоскость Е ₂ переменных х, t на четыре угла. Пусть область 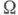представляет один из этих углов. В этом случае характеристическую задачу принято наз. задачей Гурса: определить регулярное в области W решение и( х, t).уравнения удовлетворяющее условиям

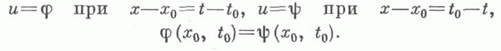
Если характеристическая поверхность Sявляется одновременно поверхностью вырождения типа или порядка, то К. х. з. может оказаться корректной. Для уравнения

к-рое является гиперболическим при y>0, линия вырождения у=0 является характеристикой. При 0<m<1 задача Коши

для уравнения (3) является корректной, а при она становится некорректной. В этом случае естественно исследовать эту задачу как с видоизмененными начальными данными:

так и с неполными начальными данными, т. е. при отсутствии одного из условий (4).

Лит.:[1] В л а д и. <м и р о в В. О., Уравнения математической физики, 3 изд., М., 1976; [2J Г о д у н о в С. К., Уравнения математической физики, М., 1971; 13] Трикоми Ф., Лекции по уравнениям в частных производных, пер. с итал., М., 1957; [4] Б е р с Л., Д ж о н Ф., Ш е х т е р М., Уравнения с частными производными, пер. с англ., М., 1966; [5] Б и ц а д з е А. В., Калиниченко Д. Ф., Сборник задач по уравнениям математической физики, М., 1977; [61 Б и ц а д з е А. В., Линейные уравнения с частными производными смешанного тина, в кн.: Тр. третьего Всесоюзного математического съезда, т. 3, М., 1958. В. А. Елеев.