ГУРСА ЗАДАЧА

- решение гиперболич. уравнения и системы 2-го порядка с двумя независимыми переменными по заданным его значениям на двух характеристич. кривых, выходящих из одной точки.

Для гиперболич. уравнения

заданного, напр., в области

Г. з. ставится следующим образом: найти регулярное в области решение уравнения (1) и непрерывное в замыкании по краевому условию

где и - заданные непрерывно дифференцируемые функции. Если функция Fнепрерывна для всех и для любой системы действительных значений переменных 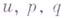и допускает производные и , к-рые при тех же условиях по абсолютной величине меньше нек-рого числа, то в области существует единственное и устойчивое решение задачи (1), (2). При исследовании Г. з. в линейном случае

фундаментальную роль играет функция Римана , к-рая однозначно определяется как решение уравнения

удовлетворяющее на характеристиках и условию

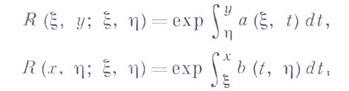
где 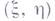- произвольная точка из области задания уравнения (3). Если функции 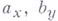и снепрерывны, то функция Рнмана существует и по переменным является решением уравнения .

Решение Г. з. (2) для уравнения (3) дается так наз. формулой Римана. При она имеет вид:

Из формулы Римана следует, что значение решения Г. з. в точке зависит лишь от значения заданных функций в характеристич. четырехугольнике При это значение зависит лишь от значения функции y(x) и j(у)в промежутках 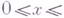и соответственно, а при функция

Метод получения явных формул решения Г. з. с помощью функции Римана известен под названием метода Римана. Этот метод распространен на довольно широкий класс гиперболич. систем 1-го н 2-го порядков. В частности, на систему вида (3), где а, b и с - квадратные симметрия, матрицы порядка п, а fи и - векторы с пкомпонентами.

Непосредственным обобщением Г. з. является задача Дарбу- Пикара, к-рая состоит в определении решения гпперболич. уравнения и системы 2-го порядка с двумя независимыми переменными по заданным его значениям на двух гладких монотонных кривых g и d, выходящих из одной точки Аи расположенных в характеристич. угле с вершиной в точке А. В частности, g и dмогут частично или полностью совпадать со сторонами этого угла. Эта задача исследована для уравнения вида (1).

Г. з. иногда наз. задачей Дарбу. Под Г. з. для гиперболич. уравнений 2-го порядка с несколькими независимыми переменными часто понимают характеристич. задачу, т. е. задачу отыскания решения по заданным его значениям на характеристич. коноиде (см. Дифференциальные уравнения с частными производными;задача с данными на характеристиках).

Г. з. названа по имени Э. Гурса (Е. Goursat), подробно ее исследовавшего.

Лит.:[1] Гурса 9., Курс математического анализа, пер. с франц., т. 3, ч. 1, М.-Л., 1933; [2] Бицадзе А. В., Уравнения смешанного типа, М., 1959; [3] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [4] Трикоми Ф., Лекции по уравнениям в частных производных, пер. с итал., М., 1957. А. М. Нахушев.