ТИХОНОВСКИЙ КУБ

- топологич. произведение экземпляров обычного отрезка I действительной прямой, где - произвольный кардинал; обозначается 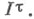Т. к. введен А. Н. Тихоновым в 1929. Если 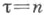- натуральное число, то Т. к. 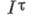есть единичный куб в re-мерном евклидовом пространстве, топология к-рого порождена метрикой скалярного произведения. Если 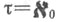- мощность натурального ряда, то куб гомеоморфен гильбертову кирпичу. При Т. к. и не гомеоморфны между собой: если - бесконечный кардинал, то есть вес пространства а если 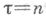- натуральное число, то п - размерность пространства I ^п. Два свойства Т. к. особенно важны: бикомпактность каждого из них, независимо от и их универсальность по отношению ко вполне регулярным T₁ -пространствам веса не большего, чем каждое такое пространство гомеоморфно нек-рому подпространству пространства Бикомпактные хаусдорфовы пространства, вес к-рых не превосходит гомеоморфны замкнутым подпространствам тихоновского куба 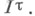Таким образом, всего двух операций - операции топологич. произведения и операции перехода к замкнутому подпространству - достаточно для того, чтобы получить из одного стандартного и весьма простого топологич. пространства - отрезка - любой бикомпакт. Примечательным следствием бикомпактности Т. к. является бикомпактность единичного шара в сопряженном к банахову пространству, наделенном слабой топологией сопряженного. Универсальность Т. к. и простота определения делает их важными стандартными объектами общей топологии. Однако топологич. строение Т. к. далеко не тривиально. 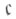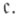В частности, куб где - мощность континуума, сепарабелен, хотя состоит из точек; вес его равен Неожиданный факт: число Суслина каждого Т. к. счетно, независимо от т. е. каждое семейство попарно непересекающихся открытых множеств в счетно. Хотя в Т. к. есть много сходящихся последовательностей, этих последних не хватает для того, чтобы описать прямо оператор замыкания в Т. К.

А. В. Архангельский.