- СИМПЛЕКТИЧЕСКАЯ СТРУКТУРА
инфинитезимальная структура1-го порядка на четномерном гладком ориентируемом многообразии М 2n, к-рая определяется заданием на М 2п невырожденной 2-формы Ф. В каждом касательном пространстве Т х( М 2n). возникает структура симплектич. пространства с кососимметрическим скалярным произведением Ф (X, Y). Все касательные к М 2n реперы, адаптированные к С. с. (т. е. реперы, относительно к-рых Ф имеет канонич. вид
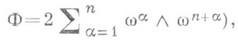
образуют главное расслоенное пространство над М 2n, структурной группой к-рого является симплектич. группа Sр(n). Вообще, задание С. с. на М 2п равносильно заданию Sp(n)-структуры на М 2n, как нек-рой G-cmpyкmypы.
На М 2n со С. с. существует изоморфизм между модулями векторных полей и 1-форм на M2n, к-рый векторному полю Xставит в соответствие 1-форму
. Образ скобки Ли [X, Y]наз. при этом скобкой Пуассона [wX, wY]; в частности, когда wX и wY полные дифференциалы, получается понятие скобки Пуассона двух функций на M2n, к-рое обобщает соответствующее классич. понятие.
С. с. наз. почти гамильтоновой структурой, а если Ф замкнута, т. е. dФ=0, то гамильтоновой структурой; впрочем, иногда условие dФ=0 включают в определение С. с. Эти структуры, находящие применения в глобальной аналитич. механике, основаны на том факте, что на касательном расслоенном пространстве Т* (М).любого гладкого многообразия Мсуществует каноническая гамильтонова структура. Она определяется формой Ф=dq, где 1-форма q на Т*(M), наз. формой Лиувилля, задается следующим образом: qu( Х и)=и(p*Х и).для любого касательного вектора Х и в точке
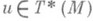, где p - проекция 
. Если на Мвыбраны локальные координаты х 1, . . ., х п и
, то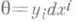 
, вследствие чего 
В классич. механике Минтерпретируется как конфигурационное пространство, а Т* (М).как фазовое пространство.
Векторное поле Xна М 2n с гамильтоновой структурой наз. гамильтоновым (или гамильтоновой системой), если 1-форма wX замкнута. Если она, кроме того, точна, т. е. wX=-dH, то функция Нна М 2п наз. гамильтонианом и является обобщением соответствующего классического понятия.
Лит.:[1] Стернберг С., Лекции по дифференциальной геометрия, пер. с англ., М., 1970; [2] Годбийон К., Дифференциальная геометрия и аналитическая механика, пер. с франц., М., 1973. Ю. Г. Лумисте.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
