СИММЕТРИЧЕСКАЯ ПРОИЗВОДНАЯ
- СИММЕТРИЧЕСКАЯ ПРОИЗВОДНАЯ
обобщение понятия производной на случай функций множества Ф в n-мерном евклидовом пространстве. С. п. в точке хесть предел
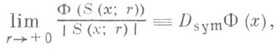
где S(х; r) - замкнутый шар с центром в точке хи радиусом r. С. п. порядка nв точке хфункции действительного переменного f(х).наз. предел
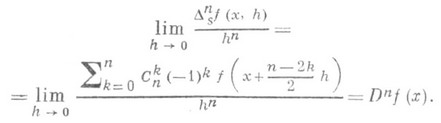
Функция действительного переменного f(х).имеет С. п. в точке хпорядка 2r:
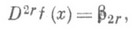
если
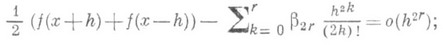
порядка 2r+1:
 если
если
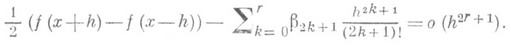
Если в точке хсуществует п-я производная f(n) (х), то в этой точке существует (в обоих смыслах) С. п. и она равна f(n) (х). Если f(х).имеет в точке хпроизводную D2rf(x). или D2r+1f(x), то она имеет производную Dnf(x). Обратное утверждение справедливо при условии существования всех производных Dnf(x).меньшего порядка той же четности.
Лит.:[1] Сакс С., Теория интеграла, пер. с англ., М., 1949; [2] James R. D., "Trans. Amer. Math. Soc.", 1954, v. 76, № 1, p. 149 - 76. Т. П. Лукашенко.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "СИММЕТРИЧЕСКАЯ ПРОИЗВОДНАЯ" в других словарях:
Производная Римана — Производная Римана, производная Шварца или вторая симметрическая производная , функции в точке предел Связанные определения Верхний и нижний пределы … Википедия
ШВАРЦА СИММЕТРИЧЕСКАЯ ПРОИЗВОДНАЯ — функции f(x)в точке x0 величина иногда наз. производной Римана, или второй симметрической производной. Впервые введена Б. Риманом в 1854 (см. [2]), рассматривалась Г. Шварцем [1]. Более общо Ш. с. п. называют симметрич. производную порядка п Лum … Математическая энциклопедия
РИМАНА ПРОИЗВОДНАЯ — производная Шварца, вторая симметрическая производная, функции f (х)в точке х 0 предел Введена Б. Риманом (В. Riemann, 1854); он доказал, что если в точке х 0 существует 2 я производная f (x0),то существует Р. п. и . Верхний и нижний пределы при… … Математическая энциклопедия
ВАЛЛЕ ПУССЕНА ПРОИЗВОДНАЯ — обобщенная симметрическая производная; определена Ш. Балле Пуссеном [1]. Пусть г четное и пусть существует такое, что для всех где постоянные, при и Тогда число наз. производной Балле Пуссена порядка r, иначе сим … Математическая энциклопедия
Тензорное исчисление — математическая теория, изучающая величины особого рода тензоры, их свойства и правила действий над ними. Т. и. является развитием и обобщением векторного исчисления (См. Векторное исчисление) и теории матриц (См. Матрица). Т. и. широко… … Большая советская энциклопедия
Гессиан функции — Гессиан функции симметрическая квадратичная форма[источник?], описывающая поведение функции во втором порядке. Для функции , дважды дифференцируемой в точке или где … Википедия
Матрица Гессе — Гессиан функции симметрическая квадратичная форма описывающая поведение функции во втором порядке. Для функции f дважды дифференцируемой в точке или где (или … Википедия
Определитель Гессе — Гессиан функции симметрическая квадратичная форма описывающая поведение функции во втором порядке. Для функции f дважды дифференцируемой в точке или где (или … Википедия
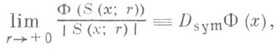
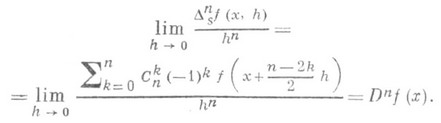
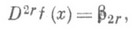
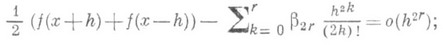
 если
если