СИММЕТРИЧЕСКАЯ ОБЛАСТЬ

- комплексное многообразие D, изоморфное ограниченной области в , для каждой точки рк-рого существует инволютивное голоморфное преобразование s _р: DD, имеющее рединственной неподвижной точкой. С. о. является эрмитовым симметрич. пространством отрицательной кривизны относительно метрики Бергмана. Группа ее автоморфизмов как комплексного многообразия содержится в группе движений и имеет ту же связную компоненту G(D), к-рая является некомпактной вещественной полупростой группой Ли без центра. Стационарная подгруппа Н(D).точки в группе G(D).есть связная компактная группа Ли с одномерным центром. Как вещественное многообразие С. о. диффеоморфна .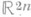

Всякая С. о. единственным образом разлагается в прямое произведение неприводимых С. о., перечисленных в следующей таблице (где М _р,q обозначает пространство комплексных матриц размера ).

С. о. типа III может быть представлена как верхняя полуплоскость Зигеля:

Ее точки параметризуют главно поляризованные абелевы многообразия. Остальные С. о. также могут быть представлены как Зигеля области первого или второго рода (см. [2]).

Лит.:[1] 3игель К., Автоморфные функции нескольких комплексных переменных, пер. с англ., М., 1954; [2] Пятецкий-Шапиро И. И., Геометрия классических областей и теория автоморфных функций, М., 1961; [3] Cartan E., "Abh. Math. Sem. Univ. Hamburg", 1935, Bd 1, S. 116-62; [4] Drucker D., Exceptional Lie algebras and the structure of hermitian symmetric spaces, Providence, 1978 (Mem. Amer. Math. Soc., v. 16, № 208). Э. Б. Винберг.