СВЯЗКА ПОЛУГРУПП

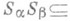
данного семейства {S_a} - полугруппа S, обладающая разбиением на подполугруппы, классы к-рого суть в точности полугруппы S_a, и для любых S_a,S_b существует S_g такая, что . В этом случае говорят также, что S разложима в связку полугрупп S_a.. Другими словами, S есть С. п. S_a, если все S_a- подполугруппы в S и существует конгруэнция r на S такая, что r-классы суть в точности S_a.. Полугруппы S_a наз. к о м п о н е н т а м и данной связки. Термин "С. п." согласуется с использованием нередко слова "связка" как синонима термина "полугруппа идемпонентов", так как конгруэнция r на полугруппе S определяет разложение S в связку тогда и только тогда, когда факторполугруппа S/r - полугруппа идемпотентов.

Многие полугруппы разложимы в связку полугрупп с теми или иными "более хорошими" свойствами; таким образом, изучение их строения в известной мере сводится к рассмотрению типов, к к-рым принадлежат компоненты связки, и к рассмотрению полугрупп идемпотентов (см., напр., Архимедова полугруппа, Вполне простая полугруппа, Клиффордова полугруппа, Периодическая полугруппа, Сепаративная полугруппа).

С. п. S_a наз. к о м м у т а т и в н о й, если для соответствующей конгруэнции r факторполугруппа S/rкоммутативна; тогда S/r - полурешетка (в этом случае часто говорят, что S есть полурешетка полугрупп S_a, в частности, если S/r - цепь, то говорят, что S есть цепь полугрупп S_a). С . п. наз. прямоугольной (иногда - м а т р и ч н о й), если S/r - прямоугольная полугруппа (см. Идемпотентов полугруппа). Это эквивалентно тому, что компоненты связки могут быть индексированы парами индексов S_il, где i и lпробегают нек-рые множества I и соответственно, причем для любых S_il, S_jm выполняется включение . Любая С. п. есть полурешетка прямоугольных связок, т. е. ее компоненты могут быть распределены на подсемейства так, что объединение компонент каждого подсемейства есть прямоугольная связка этих компонент, а исходная полугруппа разложима в полурешетку указанных объединений (теорема Клиффорда [1]). Поскольку свойства быть полугруппой идемпотентов, полурешеткой, прямоугольной полугруппой характеризуются тождествами, на любой полугруппе S для каждого из перечисленных свойств q существует наименьшая конгруэнция, для к-рой соответствующая факторполугруппа обладает свойством q, т. е. существуют наибольшие (или наиболее дробные) разложения S в С. п., в коммутативную С. п., в прямоугольную С. п.

К специальным типам С. п. относится сильная связка [4]: для любых элементов аи bиз разных компонент произведение аb равно степени одного из этих элементов. Важным частным случаем сильной связки и одновременно частным случаем цепи полугрупп является о р д и н а л ь н а я с у м м а (или последовательно аннулирующая связка): множество ее компонент {S_a}линейно упорядочено и для любых S_a, S_b таких, что S_a < S_b, и любых , имеет место равенство аb=bа=а. Заданием компонент и способа их упорядочения ординальная сумма определяется однозначно с точностью до изоморфизма.

Лит.: [1] C l i f f o r d А., "Ргос. Аmег. Маth. Sос.", 1954, v. 5, р. 499-504; [2] К л и ф ф о р д А., П р е с т о н Г., Алгебраическая теория полугрупп, пер. с англ., т. 1, М., 1972; [3] Л я п и н Е. С., Полугруппы, М., 1960; [4] Ш е в р и н Л. Н., "Изв. вузов. Матем.", 1965, № 6, с. 156-65. Л. Н. <Шеврин.