ПЕРИОДИЧЕСКАЯ ПОЛУГРУППА

полугруппа, в к-рой каждая моногенная подполугруппа конечна (другими словами, каждый элемент имеет конечный порядок). Всякая П. п. имеет идемпотенты. Множество К _е всех элементов П. п., нек-рая (зависящая от элемента) степень к-рых равна данному идемпотенту е, наз. классом кручения, соответствующим этому идемпотенту. Множество G_e всех элементов из К _е, для к-рых еслужит единицей, является -классом (см. Грина отношения эквивалентности), наибольшей подгруппой в К _е и идеалом в подполугруппе <К _е>, порожденной К _е;. т-аким образом < К _е> будет гомогруппой (см. Минимальный идеал). П. п. с единственным идемпотентом наз. унипотентной. Унипотентность П. п. Sэквивалентна каждому из следующих условий: Sесть идеальное расширение группы при помощи нильполугруппы, S есть подпрямое произведение группы и нильполугруппы.

Разбиение П. п. на классы кручения играет определяющую роль при изучении многих вопросов для периодич. полугрупп. Произвольный класс кручения не обязательно является подполугруппой: минимальный контрпример - пятиэлементная Брандта полугруппа В₂, изоморфная рисовской полугруппе матричного типа над единичной группой с единичной сэндвич-матрицей 2-го порядка. В П. п. S все классы кручения будут подполугруппами тогда и только тогда, когда Sне содержит подполугруппы, являющейся идеальным расширением унипотентной полугруппы при помощи В ₂; в этом случае разбиение Sна классы кручения не обязательно будет связкой. Известны различные (в том числе необходимые и достаточные) условия, при к-рых П. п. есть связка классов кручения; это, очевидно, имеет место для коммутативных полугрупп, это верно для П. п. с двумя идемпотентами [3].

В любой П. п. отношения Грина и 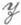совпадают; 0-простая П. п. будет вполне О-простой. Для П. п. Sследующие условия эквивалентны: 1) S - архимедова полугруппа,2) все идемпотенты из Sпопарно не сравнимы относительно естественного частичного порядка (см. Идемпотент),3) Sесть идеальное расширение вполне простой полугруппы при помощи нильполугруппы. Известно много условий, эквивалентных тому, что П. п. Sразлагается в связку (а тогда и в полурешетку) архимедовых полугрупп; среди них: 1) для любого 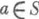' и для любого идемпо-тента 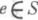, если , то 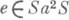(см. [5]); 2) в Sкаждый регулярный 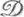-класс есть подполугруппа; 3) каждый регулярный элемент из Sявляется групповым.

Пусть S - бесконечная П. п., E_S - множество всех ее идемпотентов. Если Е _S конечно, то Sсодержит бесконечную унипотентную подполугруппу, если Е _S бесконечно, то Sсодержит бесконечную подполугруппу, являющуюся нильпотентной полугруппой или полугруппой идемпотентов [4].

Важный подкласс П. п. составляют локально конечные полугруппы. Более широкий класс составляют квазипериодич. полугруппы (Sназ. квазипериодической, если нек-рая степень каждого ее элемента лежит в подгруппе ). Многие свойства П. п. переносятся на квазипериодич. полугруппы.

Лит.:[1] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, пер. с англ., т. 1, М., 1972; [2] Ляпин Е. С., Полугруппы, М., 1960; [3] Просвиров А. С., "Матем. зап. Уральск, ун-та", 1971, т. 8, № 1, с. 77-94; [4] Шеврин Л. Н., "Изв. вузов. Математика", 1974, № 5, с. 205-15; [5] Рutсhа М.. "Semigroup Forum", 1973, v. 6, № 1, p. 12-34; [6] Schwarz St., "Чехосл. матем. ж.", 1953, т. 3, с. 7-21.

Л. Н. Шеврин.