СВОБОДНАЯ ПОЛУГРУППА

над алфавитом А - полугруппа, элементами к-рой. являются всевозможные конечные последовательности элементов из А(букв), а операция состоит в приписывании одной последовательности к другой. Элементы С. п. принято называть словами, а операцию часто называют конкатенацией. Ради удобства нередко рассматривают также и пустое слово 1 (длина к-рого по определению равна нулю), полагая w1=1w=w для любого слова w;возникающая таким образом полугруппа с единицей наз. с в о б о д н ы м м о н о и д о м над А. С . п . (свободный моноид) над Ачасто обозначают А ⁺ (соответственно А*). Для С. п. А ⁺ алфавит Аявляется единственным неприводимым порождающим множеством; он состоит в точности из элементов, неразложимых в произведение. Буквы из Аназ. свободными образующими. С. п. определяется однозначно с точностью до изоморфизма мощностью своего алфавита; эта мощность наз. рангом свободной полугруппы. С. п. ранга 2 имеет подполугруппы, являющиеся С. п. счетного ранга.

С. п. являются свободными алгебрами в классе всех полугрупп. Следующие условия для полугруппы Fэквивалентны: 1) Fесть С. п.; 2) Fимеет порождающее множество Атакое, что любой элемент из Fединственным образом представим в виде произведения элементов из А;3) Fудовлетворяет закону сокращения, не содержит идемпотентов, каждый элемент из Fимеет конечное число делителей, и для любых равенство влечет, что и=и' или один из элементов и, и' есть левый делитель другого.

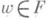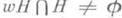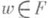Всякая подполугруппа Нв С. п. имеет единственное неприводимое порождающее множество, состоящее из элементов, неразложимых в H в произведение; однако не всякая подполугруппа С. п. сама свободна. Следующие условия для подполугруппы Нв С. п. Fэквивалентны: 1) Несть С. п.; 2) для любого из того, что и , следует, что ; 3) для любого из того, что 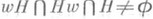, следует, что . Для произвольных различных слов и, v в С. п. Fлибо ии v являются свободными образующими порожденной ими подполугруппы, либо существует такое, что 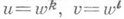для нек-рых натуральных k, l;вторая альтернатива выполняется тогда и только тогда, когда иv=vu. Всякая подполугруппа с тремя образующими в С. п. будет конечно определенной полугруппой, но существуют подполугруппы с четырьмя образующими, не являющиеся конечно определенными.

С. п. естественно возникают в автоматов алгебраической теории (см. также [5], [6]), теории кодирования (см. Кодирование алфавитное,[4] - [6]), теории формальных языков и формальных грамматик (см. [3], [5], [6]). С указанными областями связана проблематика решения уравнений в С. п. (см. [7] - [9]). Существует алгоритм, распознающий разрешимость произвольных уравнений в С. п.

Лит.:[1] К л и ф ф о р д А., П р е с т о н Г., Алгебраическая теория полугрупп, пер. с англ., т. 1-2, М., 1972; [2] Л я п и н Е. С., Полугруппы, М., 1960; [3] Г р о с с М., Л а н т е н А., Теория формальных грамматик, пер. с франц., М., 1971; [4] М а р к о в А. А., Введение в теорию кодирования, М., 1982; [5] Е i 1 е n b е r g S., Аutоmаtа, lаnguages аnd mа-chines, v. А-В, N. Y.-L., 1974-76; [6] L а 1 1 е m е n t G., Semigroups аnd соmbinatoriа1 арplications, N. Y.- [а. о.], 1979; [7] L е n t i n А., Еquations dans 1еs mоnoides libres, Р., 1972; [8] X м е л е в с к и й Ю. И., Уравнения в свободной полугруппе, М., 1971 (Тр. Матем. ин-та АН СССР, т. 107); [9] М а к а н и н Г. С., "Матем. сб.", 1977, т. 103, № 2, с. 147- 236. Л. Н. Шеврин.