СВОБОДНАЯ АЛГЕБРА

к л а с с а универсальных алгебр - алгебра Fиз класса , обладающая с в о б о д н о й п о р о ж д а ю щ е й с и с т е м о й (или б а з о й) X, т. е. таким множеством порождающих X, что всякое отображение множества Xв любую алгебру Аиз продолжается до гомоморфизма алгебры Fв А(ср. Свободная алгебраическая система). С . а. обладает любой непустой класс алгебр, замкнутый относительно подалгебр и прямых произведений и содержащий неодноэлементные алгебры. В частности, С. а. всегда существует в нетривиальных многообразиях и квазимногообразиях универсальных алгебр (см. Универсальных алгебр многообразие, Алгебраических систем квазимногообразие). С. а. класса, состоящего из всех алгебр данной сигнатуры 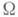, наз. а б с о л ю т н о с в о б о д н о й. Алгебра Асигнатуры является С. а. нек-рого класса универсальных алгебр сигнатуры тогда и только тогда, когда A внутренне свободна, т. е. обладает таким порождающим множеством X, что всякое отображение Xв Апродолжается до эндоморфизма алгебры А. Если С. а. обладает бесконечной базой, то все ее базы имеют одну и ту же мощность (см. Свободная абелева группа, Свободная алгебра над ассоциативно-коммутативным кольцом, Свободная ассоциативная алгебра, Свободная булева алгебра, Свободная группа, Свободная полугруппа, Свободная решетка, Свободный группоид, Свободный модуль, а также Свободное произведение). Ясно, что каждый элемент С. а. с базой Xзаписывается как слово в алфавите Xвсигнатуре рассматриваемого класса. Естествен вопрос: когда различные слова равны как элементы С. а.? В нек-рых случаях ответ почти тривиален (полугруппы, кольца, группы, ассоциативные алгебры), в других - достаточно сложен (алгебры Ли, решетки, булевы алгебры), а иногда и не поддается решению (альтернативные кольца). Л. А. Скорняков.