СВОБОДНАЯ ГРУППА

- группа F с системой Xпорождающих элементов такая, что любое отображение множества Xв любую группу G продолжается до гомоморфизма Fв G. Такая система Xназ. с и с т е м о й с в о б о д н ы х п о р о ж д а ю щ и х; ее мощность наз. р а н г о м с в о б о д н о й г р у п п ы F. Множество Xназ. также а л ф а в и т о м. Элементы из Fпредставляют собой слова в алфавите X, т. е. выражения вида

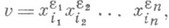
где при всех j, а также пустое слово. Слово vназ. н е с о к р а т и м ы м, если при всех j=1,2..., n-1. Несократимые слова являются разными элементами С. г. F, и каждое слово равно единственному несократимому слову. Число пназ. длиной слова v,если оно несократимо. П р е о б р а з о в а н и я м и Н и л ь с е н а конечного упорядоченного множества элементов группы называются: 1) перестановка двух элементов в этом множестве, 2) замена одного из а _i- на , 3) замена одного из a_i на a_ia_j, где 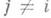. Если С. г. Fимеет конечный ранг, то преобразования Нильсена над системой свободных порождающих приводят к новым системам свободных порождающих, причем любая система свободных порождающих может быть получена из любой другой последовательности применением этих преобразований (т е о р е м а Н и л ь с е н а, см. [2]). Значение С. г. определяется тем, что всякая группа изоморфна нек-рой факторгруппе подходящей С. г. Всякая подгруппа С. г. также свободна (теорема Нильсена -Шрайера, см. [1], [2]).

С. г. групп многообразияопределяется аналогично С. г., но в пределах 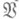. Ее наз. также 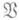-свободной группой, или относительно свободной (а также п р и в е д е н н о с в о б о д н о й). Если 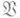определяется системой тождеств v=1, где , то С. г. многообразия с системой Xсвободных порождающих изоморфна факторгруппе F/V(F)С. г. Fс системой Xсвободных порождающих по вербальной подгруппе V(F) - подгруппе, порожденной всеми значениями слов в F. С. г. нек-рых многообразий имеют специальные названия, напр.: свободная абелева, свободная нильпотентная, свободная разрешимая, свободная бернсайдова - С. г. многообразий 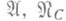, соответственно.

Лит.:[1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967; [2] М а г н у с В., К а р р а с А., С о л и т э р Д., Комбинаторная теория групп, пер. с англ., М., 1974; [3] Н е й м а н X., Многообразия групп, пер. с англ., М., 1969.

А. Л. Шмелъкин.