- РАЦИОНАЛЬНОЕ ОТОБРАЖЕНИЕ
- обобщение понятия рациональной функции на алгебраич. многообразии. А именно, р а ц и о н а л ь н ы м о т о бр а ж е н и е м неприводимого алгебраич. многообразия Xв алгебраич. многообразие Y(оба определены над полем k). наз. класс эквивалентности пар (U,jU), где U - непустое открытое подмножество в X, а jU- морфизм из Uв Y. При этом пары (U,jU). и (V, jV) считаются эквивалентными, если jU и jV совпадают на
 . В частности, Р. о. многообразия X в аффинную прямую есть рациональная функция на многообразии X. Для каждого Р. о. j :
. В частности, Р. о. многообразия X в аффинную прямую есть рациональная функция на многообразии X. Для каждого Р. о. j :  существует такая пара
существует такая пара  , что
, что  для любой эквивалентной ей пары (U,jU) и jU является ограничением
для любой эквивалентной ей пары (U,jU) и jU является ограничением  на U.
на U.
Открытое подмножество
 наз. о б л а с т ь ю р е г ул я р н о с т и Р. о. j, а
наз. о б л а с т ь ю р е г ул я р н о с т и Р. о. j, а 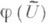 - о б р а з о м м н ог о о б р а з и я X(обозначается j(X)) при Р. о. j. Если
- о б р а з о м м н ог о о б р а з и я X(обозначается j(X)) при Р. о. j. Если  Р. о. алгебраич. многообразий и образ j (X) плотен в Y, то j определяет вложение полей
Р. о. алгебраич. многообразий и образ j (X) плотен в Y, то j определяет вложение полей  . Обратно, вложение полей рациональных функций
. Обратно, вложение полей рациональных функций  определяет Р. о. многообразия Xв Y. Если Р. о. j индуцирует изоморфизм полей рациональных функций k(X)и k (Y), то j наз. б и р а ц и о н а л ь н ы м отображением.
определяет Р. о. многообразия Xв Y. Если Р. о. j индуцирует изоморфизм полей рациональных функций k(X)и k (Y), то j наз. б и р а ц и о н а л ь н ы м отображением.
Множество точек из X, в к-рых Р. о.
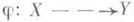 не регулярно, имеет в общем случае коразмерность 1. Но если Y - полное многообразие, а X - гладкое неприводимое многообразие, то множество точек из X, в к-рых j не регулярно, имеет коразмерность не меньше двух. Если X и Y - полные неприводимые многообразия над алгебраически замкнутым полем характеристики 0, то Р. о.
не регулярно, имеет в общем случае коразмерность 1. Но если Y - полное многообразие, а X - гладкое неприводимое многообразие, то множество точек из X, в к-рых j не регулярно, имеет коразмерность не меньше двух. Если X и Y - полные неприводимые многообразия над алгебраически замкнутым полем характеристики 0, то Р. о. может быть включено в коммутативную диаграмму (см. [2]):
может быть включено в коммутативную диаграмму (см. [2]):
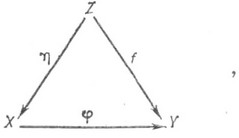 (*)
(*)
где h, f - морфизмы алгебраич. многообразия Z, и h является композицией моноидальных преобразований. Если
 - бирациональное отображение полных неособых поверхностей, то существует диаграмма (*), в к-рой оба морфизма f и hявляются композициями моноидальных преобразований с неособыми центрами (т е о р е м а З а р и с к о г о), т. е. любое бирациональное отображение полных неособых поверхностей раскладывается в композицию моноидальных преобразований с неособыми центрами и обратных к ним отображений. В случае
- бирациональное отображение полных неособых поверхностей, то существует диаграмма (*), в к-рой оба морфизма f и hявляются композициями моноидальных преобразований с неособыми центрами (т е о р е м а З а р и с к о г о), т. е. любое бирациональное отображение полных неособых поверхностей раскладывается в композицию моноидальных преобразований с неособыми центрами и обратных к ним отображений. В случае  аналогичный вопрос о разложении бирационального отображения открыт (1983).
аналогичный вопрос о разложении бирационального отображения открыт (1983).
Лит.:[1] Ш а ф а р е в и ч И. Р., Основы алгебраической геометрии, М., 1972; [2] Н i r о n a k a H., "Ann. Math.", 1964, v. 79, № 1 - 2, p. 109 -326. Buк. С. Куликов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
