БИРАЦИОНАЛЬНОЕ ОТОБРАЖЕНИЕ
- БИРАЦИОНАЛЬНОЕ ОТОБРАЖЕНИЕ
бирациональный изоморфизм,- рациональное отображение алгебраич. многообразий, индуцирующее изоморфизм их полей рациональных функций. В более общем смысле, рациональное отображение схем  наз. бирациональным отображение м, если оно удовлетворяет одному из. следующих эквивалентных условий: а) существуют такие плотные открытые множества
наз. бирациональным отображение м, если оно удовлетворяет одному из. следующих эквивалентных условий: а) существуют такие плотные открытые множества  , что
, что 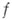 определено на
определено на  и осуществляет изоморфизм подсхем
и осуществляет изоморфизм подсхем  б) если
б) если  - множества общих точек неприводимых компонент соответственно схем
- множества общих точек неприводимых компонент соответственно схем 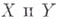 , то f индуцирует биективное соответствие множеств
, то f индуцирует биективное соответствие множеств  и изоморфизм .локальных колец
и изоморфизм .локальных колец  для каждого
для каждого  .
.
Если схемы 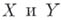 неприводимы и приведены, то локальные кольца их общих точек отождествляются с полями рациональных функций соответственно на
неприводимы и приведены, то локальные кольца их общих точек отождествляются с полями рациональных функций соответственно на 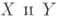 В этом случае Б. о. f:
В этом случае Б. о. f:  индуцирует, согласно условию б), изоморфизм полей рациональных функций:
индуцирует, согласно условию б), изоморфизм полей рациональных функций:
Схемы 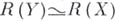 Xи Yназ. бирационально эквивалентными, или бирационально изоморфными, если существует Б. о.
Xи Yназ. бирационально эквивалентными, или бирационально изоморфными, если существует Б. о.  . Частный случай Б. о.- бирационалъный морфизм.
. Частный случай Б. о.- бирационалъный морфизм.
Простейшим Б. о. является моноидалъное преобразование с неособым центром. Для гладких полных многообразий размерности 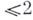 всякое Б. о. может быть представлено в виде композиции таких преобразований и обратных к ним. В общем случае вопрос остается (к 1977) открытым.
всякое Б. о. может быть представлено в виде композиции таких преобразований и обратных к ним. В общем случае вопрос остается (к 1977) открытым.
Лит.:[1] Шафаревич II. Р., Основы алгебраической геометрии, М., 1972. И. В. Долгачее, В. А. Исковских.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "БИРАЦИОНАЛЬНОЕ ОТОБРАЖЕНИЕ" в других словарях:
БИРАЦИОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ — бирациональное отображение алгебраич. многообразия (или схемы) в себя. Б. п. иногда наз. также бирациональными автоморфизмами. Группа всех Б. п. алгебраич. .многообразия канонически изоморфна группе автоморфизмов его поля рациональных функций над … Математическая энциклопедия
РАЦИОНАЛЬНОЕ ОТОБРАЖЕНИЕ — обобщение понятия рациональной функции на алгебраич. многообразии. А именно, р а ц и о н а л ь н ы м о т о бр а ж е н и е м неприводимого алгебраич. многообразия Xв алгебраич. многообразие Y(оба определены над полем k). наз. класс эквивалентности … Математическая энциклопедия
ОСНОВНОГО ТИПА АЛГЕБРАИЧЕСКАЯ ПОВЕРХНОСТЬ — общего типа алгебраическая поверхность, поверхность одного из самых обширных классов алгебраических поверхностей в классификации Энрикеса. А именно, гладкая проективная поверхность Xнад алгебраически замкнутым Полем k наз. О. т. а. п., если где… … Математическая энциклопедия
КУБИЧЕСКАЯ ГИПЕРПОВЕРХНОСТЬ — проективное алгебраич. многообразие, задаваемое однородным уравнением 3 й степени с коэффициентами из нек рого основного поля k. Кубические кривые. Неприводимая кубич. кривая является либо гладкой (в этом случае ее канонич. класс равен 0, а род… … Математическая энциклопедия
CEILIDH — криптосистема с открытым ключом, в основе которой лежат задачи дискретного логарифмирования и алгебраические группы. Впервые эта идея была предложена Алисой Силверберг и Карлом Рубин в 2003 году. Главное преимущество схемы уменьшенный размер… … Википедия
КАНОНИЧЕСКОЕ ПОГРУЖЕНИЕ — отображение алгебраич. многообразия Xв проективное пространство с помощью степеней канонического класса Кх (см. Линейная система). Пусть X неособая проективная кривая рода g;отображение, определяемое классом пКу, будет вложением для нек рого… … Математическая энциклопедия
Преобразование — одно из основных понятий математики, возникающее при изучении соответствий между классами геометрических объектов, классами функций и т.п. Например, при геометрических исследованиях часто приходится изменять все размеры фигур в одном и… … Большая советская энциклопедия
 наз. бирациональным отображение м, если оно удовлетворяет одному из. следующих эквивалентных условий: а) существуют такие плотные открытые множества
наз. бирациональным отображение м, если оно удовлетворяет одному из. следующих эквивалентных условий: а) существуют такие плотные открытые множества  , что
, что 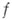 определено на
определено на  и осуществляет изоморфизм подсхем
и осуществляет изоморфизм подсхем  б) если
б) если  - множества общих точек неприводимых компонент соответственно схем
- множества общих точек неприводимых компонент соответственно схем 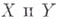 , то f индуцирует биективное соответствие множеств
, то f индуцирует биективное соответствие множеств  и изоморфизм .локальных колец
и изоморфизм .локальных колец  для каждого
для каждого  .
.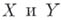 неприводимы и приведены, то локальные кольца их общих точек отождествляются с полями рациональных функций соответственно на
неприводимы и приведены, то локальные кольца их общих точек отождествляются с полями рациональных функций соответственно на 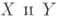 В этом случае Б. о. f:
В этом случае Б. о. f:  индуцирует, согласно условию б), изоморфизм полей рациональных функций:
индуцирует, согласно условию б), изоморфизм полей рациональных функций: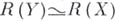 Xи Yназ. бирационально эквивалентными, или бирационально изоморфными, если существует Б. о.
Xи Yназ. бирационально эквивалентными, или бирационально изоморфными, если существует Б. о.  . Частный случай Б. о.- бирационалъный морфизм.
. Частный случай Б. о.- бирационалъный морфизм.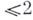 всякое Б. о. может быть представлено в виде композиции таких преобразований и обратных к ним. В общем случае вопрос остается (к 1977) открытым.
всякое Б. о. может быть представлено в виде композиции таких преобразований и обратных к ним. В общем случае вопрос остается (к 1977) открытым.