ПРОСТОЙ ИДЕАЛ

- двусторонний идеал Ркольца Rтакой, что из 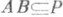, где Аи В - идеалы в R, следует, что либо , либо . Для ассоциативного кольца экливалентным определением на языке элементов будет следующее:

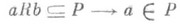или ,

где а, b - элементы кольца R. Всякий примитивный идеал прост.

Пусть R - ассоциативно-коммутативное кольцо с единицей. Тогда простота идеала эквивалентна тому, что или , т. е. тому, что фактор-кольцо R/Р есть область целостности. В этом случае всякий максимальный идеал прост, а пересечение всех простых идеалов кольца Rявляется радикалом нулевого идеала (т. е. множеством нильпотентных элементов).

Обобщением понятия П. и. служит понятие примарного идеала. В теории примарных разложений П. и. играют ту же роль, что простые числа в разложении целых чисел по степеням простых, а примерные идеалы - роль степеней простых чисел.

Идеал Ррешетки Lназ. простым, ес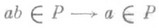ли

или .

Идеал Рпрост тогда и только тогда, когда F=LP - простой фильтр, т. е. если или

Лит.:[1] Бурбаки Н., Коммутативная алгебра, пер. с франц., М., 1971; [2] Дженобсон Н., Строение колец, пер. с англ., М., 1961; [3] 3арисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 1, М., 1063; [4] Скорняков Л. А., Элементы теории структур, М., 1970.

О. А. Иванова.