ПРОГОНКИ МЕТОД

- метод переноса одноточечного граничного условия с помощью дифференциального или разностного уравнения, соответствующего данному уравнению. Применяется для решения граничной задачи в том случае, когда пристрелки метод не эффективен.

Пусть на отрезке задано линейное обыкновенное дифференциальное уравнение

(1)

где квадратная матрица (х).порядка n и вектор f(x) - известные непрерывные функции, дифференцируемая вектор-функция у(х) = подлежит определению. К уравнению (1) присоединены граничные условия в форме

(2)

где известные матрицы j и y имеют размеры nx kи n x l и ранги k и l соответственно,

Используя дифференциальные уравнения

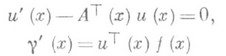
с начальными условиями u(а)=j, g(а)=a, где искомая дифференцируемая матрица-функция и(х).имеет размеры , можно определить и(х).и g(х).на всем отрезке 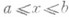(прямой ход прогонки). С помощью уравнения

и второго из граничных условий (2) можно определить значение у(b), если квадратная матрица [и(b),y] имеет ранг п. Искомое решение граничной задачи (1)-(2) вычисляется теперь как решение задачи Коши для уравнения (1) в направлении от точки х=b к точке х=а (обратный ход прогонки). Указанный метод применим и к многоточечной задаче, когда условия вида (2) задаются не только на концах, но и в нескольких внутренних точках отрезка 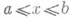Разработаны варианты метода прогонки для переноса линейных граничных условий, отличных от (2) (см. [1]).

Достоинства П. м. видны на примере следующей граничной задачи:

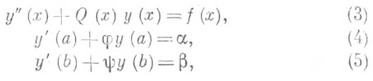
где квадратная матрица Q(x).порядка пи вектор f(х).размера п - известные непрерывные функции, дважды дифференцируемая вектор-функция у(х).подлежит определению, известные квадратные матрицы j и y имеют порядок 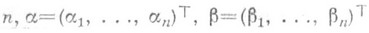Используя дифференциальные уравнения

с начальными условиями v(а)=j, g(a)=a, где искомая дифференцируемая квадратная матрица-функция v(х).имеет порядок , ищутся v(x).и g(х).на всем отрезке (прямой ход прогонки).

С помощью уравнения

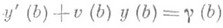
и граничного условия (5) можно определить значение

(6)

если матрица v(b) -y имеет ранг п. Искомое решение граничной задачи (3) - (5) находится как решение задачи Коши для уравнения

с начальным условием (6) (обратный ход прогонки). Таким образом, П. м. для задачи (3) - (5) является методом понижения порядка дифференциального уравнения (3).

В случае конечной последовательности линейных алгебраич. уравнений

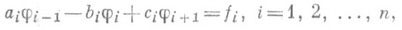(7)

где коэффициенты а _i, с _i, b_i- - известные квадратные матрицы порядка v, a f_i и j_i - известный и искомый вектор-столбцы размера v, a₁=0, с _n=0, алгоритм прогонки определяется следующим образом:

при условиях b₁=0, z₁=0 (прямой ход) и

при условии j_n+1=0 (обратный ход). Здесь b_i - квадратная матрица порядка v, z_i и j_i - вектор-столбцы размера v. Изложенный метод наз. методом правой прогонки. Аналогично формулам (8)- (10) получаются формулы левой прогонки. Комбинируя левую и правую прогонки, получают метод встречных прогонок. При решении уравнений (7) с сильно меняющимися коэффициентами применяется потоковый метод прогонки. Для нахождения периодич. решения бесконечной последовательности уравнений вида (7) с периодич. коэффициентами используется циклическая прогонка (см. [4]).

См. также Ортогональной прогонки метод.

Лит.:[1] Бахвалов Н. С., Численные Методы, 2изд., М., 1975; [2] Крылов В. И., Бобков В. В., Монастырный П. И., Вычислительные методы, т. 2, М., 1977; [3] Марчук Г. И., Методы вычислительной математики, 2 изд., М., 1980; [4] Самарский А. А., Николаев Е. С., Методы решения сеточных уравнений, М., 1978.

А. Ф. Шапкин.