МАТРИЧНОЙ ФАКТОРИЗАЦИИ МЕТОД

МАТРИЧНОЙ ФАКТОРИЗАЦИИ МЕТОД

метод матричной прогонки,- метод решения конечноразностных систем, аппроксимирующих краевые задачи для систем обыкновенных дифференциальных уравнений в одномерных задачах и для уравнений эллиптич. типа в двумерных задачах.

Решение трехточечной разностной схемы

где - искомая сеточная вектор-функция, Fi- вектор правой части, - заданные квадратные матрицы, при краевых условиях

ищется так же, как в скалярном случае, в виде

Прогоночные коэффициенты, матрица и вектор определяются рекуррентными соотношениями ("прямая прогонка")

а - левым краевым условием:

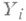считаются по формуле (*) ("обратная прогонка"), а

Устойчивость этого метода по отношению к ошибкам округления имеет место при условиях

из к-рых следует, что (см. [1]).

Имеется другая форма условий устойчивости (см. [2], [3]). М. ф. м. применяется и к двухточечным разностным схемам (см. [3]). Используется вариант, в к-ром обращение матриц заменено ортогонолизацией (см. [4]).

Лит.:[1] Самарский А. А., Введение в теорию разностных схем, М., 1971; [2] Огнева В. В., "Ж. вычисл. матем. и матем. физики", 1967, т. 7, № 4, с. 803 - 12; [3] Самарский А. А.. Николаев Е. С, Методы решения сеточных уравнений, М., 1978; [4] Годунов С. К., "Ж. вычисл. матем. и матем. физики", 1962, т. 2, .№ 6, с. 972-82.

Т. А. Гермогенова.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужна курсовая?

Полезное


Смотреть что такое "МАТРИЧНОЙ ФАКТОРИЗАЦИИ МЕТОД" в других словарях:

  • АЛЬВЕДНЫЙ МЕТОД — (в теории переноса) метод решения краевых задач для уравнения переноса. А. м. представляет собой вариант матричной факторизации, метода, когда роль коэффициентов факторизации играют матрицы отражения и пропускания последовательности слоев… …   Математическая энциклопедия

  • НЕЛИНЕЙНОЕ УРАВНЕНИЕ — численные методы решения итерационные методы решения нелинейных уравнений. Под нелинейными уравнениями понимаются (см. [1] [3]) алгебраические и трансцендентные уравнения вида где х действительное число, нелинейная функция, а под системой… …   Математическая энциклопедия

  • ПАРАБОЛИЧЕСКОГО ТИПА УРАВНЕНИЕ — численные методы решения методы решения уравнений параболич. типа на основе вычислительных алгоритмов. Для решения П. т. у. часто применяются приближенные численные методы, рассчитанные на использование быстродействующих ЭВМ. Наиболее… …   Математическая энциклопедия

  • ПУАССОНА УРАВНЕНИЕ — ; численные методы решения методы, заменяющие исходную краевую задачу для уравнения Пуассона (1) системой из Nлинейных алгебраич. уравнений LN(uN)=fN,(2) решение к рой позволяет построить нек рую аппроксимацию pNuN для решения исходной задачи, .… …   Математическая энциклопедия

  • Шрёдингер, Эрвин — Эрвин Шрёдингер Erwin Schrödinger Эрвин Шрёдингер в 1933 году Дата рожден …   Википедия

  • ФАКТОРНЫЙ АНАЛИЗ — (ф а к т о р и а л ь н ы й анализ) – один из методов математич. обработки данных исследования массовых совокупностей. При Ф. а. эти данные сводятся в корреляционные матрицы, на к рых определяются детерминанты ( факторы ), лежащие в основе… …   Философская энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»