ПРЕДСТАВЛЕНИЕ ПОЛУГРУППЫ

S в классе полугрупп X - гомоморфизм полугруппы S в нек-рую полугруппу из класса X (в случае изоморфизма говорят о точном представлении). Обычно имеются в виду классы каких-либо конкретных полугрупп. Наиболее изучены представления в классе полугрупп преобразований (короче - представления преобразованиями), в классах полугрупп частичных преобразований и бинарных отношений, в классе полугрупп матриц (т. н. матричные, или линейные, П. п.). В теории автоматов с каждым автоматом связано представление свободной полугруппы преобразованиями множества его внутренних состояний. Специальный характер носят П. п. преобразованиями, связанными тем или иным образом со свойствами элементов преобразуемого множества, наделенного какой-либо структурой (эндоморфизмами, непрерывными преобразованиями и т. п.). Всякая полугруппа с единицей изоморфно представима как полугруппа всех эндоморфизмов ориентированного или неориентированного графа, как полугруппа всех эндоморфизмов нек-рой алгебры с унарными операциями и т. п. Известно (1983) несколько конструкций, позволяющих получить все П. п. частичными преобразованиями. Они строятся из нек-рых простейших П. п. при помощи их объединения, кратного повторения, ограничения на подмножестве и операции погружения полугрупп.

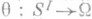Присоединив к полугруппе Sединицу: и продолжив регулярное П. п. Sлевыми сдвигами на декартову степень S^x полугруппы S¹, получают представление j_I - I-кратное повторение регулярного П. и. S. Всякое представление yполугруппы Sпреобразованиями множества W может быть получено (см. [2]) из j_I с помощью нек-рого отображения так, что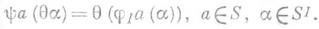

Особую роль играют транзитивные П. п., т. с. такие ее представления j преобразованиями множества W, что для любых 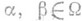найдется а, для которого (ja)a=b.

П. п. взаимно однозначными частичными преобразованиями связаны с понятием и свойствами инверсных полугрупп.

При исследовании матричных П. п. привлекаются к рассмотрению полугрупповые алгебры. Изучается вопрос о приводимости матричных П. п. Найдены неприводимые представления для ряда полугрупп (в том числе и для конечных). Матричные представления вполне простых и вполне 0-простых полугрупп могут быть построены как продолжение представлений их подгрупп.

Матричные представления произвольных полугрупп могут быть описаны при помощи представлений их факторов, являющихся простыми и 0-простыми полугруппами.

Лит.:[1] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, пер. с англ., т. 1-2, М., 1972; [2] Вагнер В. В., "Матем. сб.", 1956, т. 38, .№2, с. 203-40; [3] Ляпин Е. С., там же, 1960, т. 52, № 1, с. 589-96; [4] Шайн Б. М., там же, 1963, т. 60, JM5 3, с. 293-303; [5] МсА1istеr D. В., "Semigroup Forum", 1971, v. 2, № 3, p. 189- 203; №4, p. 288-320; [6] Jоnssоn В., Topics in universal algebra. В. -N. Y., 1972. Л. М. Глускин, Е. С. Л япин.