НЕПРИВОДИМОЕ ПРЕДСТАВЛЕНИЕ
- НЕПРИВОДИМОЕ ПРЕДСТАВЛЕНИЕ
- (линейное) представление  группы (алгебры, кольца, полугруппы) Xв векторном пространстве (или топологическом векторном пространстве) Е, единственными (замкнутыми) инвариантными подпространствами к-рого являются
группы (алгебры, кольца, полугруппы) Xв векторном пространстве (или топологическом векторном пространстве) Е, единственными (замкнутыми) инвариантными подпространствами к-рого являются 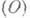 и
и 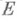 . Часто Н. п. в топологическом векторном пространстве наз. топологически неприводимым представлением; если
. Часто Н. п. в топологическом векторном пространстве наз. топологически неприводимым представлением; если  - представление в топологическом векторном пространстве Е, являющееся Н. п. как представление в векторном пространстве Е, то представление я наз. алгебраически неприводимым представлением. Алгебраически Н. п. является топологически Н. п.; обратное, вообще говоря, неверно. Есть ряд понятий, близких к понятию Н. п., в том числе - операторно неприводимое представление, вполне неприводимое представление (представление, семейство операторов к-рого образует вполне неприводимое множество). Вполне Н. п. является (топологически) Н. п. и операторно Н. п.; обратные утверждения, вообще говоря, неверны.
- представление в топологическом векторном пространстве Е, являющееся Н. п. как представление в векторном пространстве Е, то представление я наз. алгебраически неприводимым представлением. Алгебраически Н. п. является топологически Н. п.; обратное, вообще говоря, неверно. Есть ряд понятий, близких к понятию Н. п., в том числе - операторно неприводимое представление, вполне неприводимое представление (представление, семейство операторов к-рого образует вполне неприводимое множество). Вполне Н. п. является (топологически) Н. п. и операторно Н. п.; обратные утверждения, вообще говоря, неверны.
А. И. Штерн.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "НЕПРИВОДИМОЕ ПРЕДСТАВЛЕНИЕ" в других словарях:
Неприводимое представление — Представление группы, точнее линейное представление группы гомоморфизм заданной группы в группу невырожденных линейных преобразований векторного пространства. Образ этого гомоморфизма сам является группой, элементами которой являются… … Википедия
ОПЕРАТОРНО НЕПРИВОДИМОЕ ПРЕДСТАВЛЕНИЕ — представление p группы (алгебры, кольца, полугруппы) Xв (топологическом) векторном пространстве Етакое, что любой (непрерывный) линейный оператор в пространстве Е, перестановочный со всеми операторами (х), , кратен единичному оператору в Е. Если… … Математическая энциклопедия
ПРЕДСТАВЛЕНИЕ ГРУППЫ — изображение элементов группы матрицами или преобразованиями линейного пространства, при к ром сохраняется исходная групповая структура. Поскольку достаточно хорошо изучены матричные группы, при исследовании произвольной группы стараются… … Физическая энциклопедия
ПРЕДСТАВЛЕНИЕ ТОПОЛОГИЧЕСКОЙ ГРУППЫ — непрерывное отображение группы G в топологич. группу гомеоморфизмов нек рого топологич. пространства. Чаще всего под П. т. г. Gпонимается линейное представление, более того такое линейное представление л топологич. группы G в топологич. векторном … Математическая энциклопедия
Представление группы — У этого термина существуют и другие значения, см. Представление. Не следует путать с заданием группы. Представление группы (точнее, линейное представление группы) гомоморфизм заданной группы в группу невырожденных линейных преобразований… … Википедия
ПРЕДСТАВЛЕНИЕ СО СТАРШИМ ВЕКТОРОМ — линейное представление r конечномерной полупростой расщепляемой алгебры Ли над полем kхарактеристики нуль с расщепляющей Картана подалгеброй t, удовлетворяющее следующим условиям. 1) В пространстве Vпредставления r существует циклический вектор v … Математическая энциклопедия
ПРЕДСТАВЛЕНИЕ СИММЕТРИЧЕСКОЙ ГРУППЫ — линейное представление группы Sm над каким либо полем К. Если char K=0, то все конечномерные П. с. г. вполне приводимы и определены над Q (иначе говоря, все неприводимые конечномерные представления над Q абсолютно неприводимы). Неприводимые… … Математическая энциклопедия
ИНДУЦИРОВАННОЕ ПРЕДСТАВЛЕНИЕ — представление p локально компактной группы G, индуцированное представлением р ее замкнутой подгруппы Н, точнее, представление p группы Gв нек ром пространстве Ефункций f на группе G, принимающих значения в пространстве Vпредставления р и… … Математическая энциклопедия
ПРЕДСТАВЛЕНИЕ АЛГЕБРЫ ЛИ — в векторном пространстве V гомоморфизм r алгебры Ли Lнад полем kв алгебру Ли всех линейных преобразований пространства Vнад k. Два представления и наз. эквивалентными (или изоморфными), если существует изоморфизм , для к рого a(r1 (l) v1).r2(l)a… … Математическая энциклопедия
ПРЕДСТАВЛЕНИЕ КОМПАКТНОЙ ГРУППЫ — гомоморфизм компактной группы в группу непрорывных линейных автоморфизмов (комплексного) банахова пространства, непрерывный в сильной операторной топологии. Пусть G компактная группа, V банахово пространство и представление. Если V=H гильбертово… … Математическая энциклопедия
 группы (алгебры, кольца, полугруппы) Xв векторном пространстве (или топологическом векторном пространстве) Е, единственными (замкнутыми) инвариантными подпространствами к-рого являются
группы (алгебры, кольца, полугруппы) Xв векторном пространстве (или топологическом векторном пространстве) Е, единственными (замкнутыми) инвариантными подпространствами к-рого являются 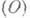 и
и 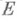 . Часто Н. п. в топологическом векторном пространстве наз. топологически неприводимым представлением; если
. Часто Н. п. в топологическом векторном пространстве наз. топологически неприводимым представлением; если  - представление в топологическом векторном пространстве Е, являющееся Н. п. как представление в векторном пространстве Е, то представление я наз. алгебраически неприводимым представлением. Алгебраически Н. п. является топологически Н. п.; обратное, вообще говоря, неверно. Есть ряд понятий, близких к понятию Н. п., в том числе - операторно неприводимое представление, вполне неприводимое представление (представление, семейство операторов к-рого образует вполне неприводимое множество). Вполне Н. п. является (топологически) Н. п. и операторно Н. п.; обратные утверждения, вообще говоря, неверны.
- представление в топологическом векторном пространстве Е, являющееся Н. п. как представление в векторном пространстве Е, то представление я наз. алгебраически неприводимым представлением. Алгебраически Н. п. является топологически Н. п.; обратное, вообще говоря, неверно. Есть ряд понятий, близких к понятию Н. п., в том числе - операторно неприводимое представление, вполне неприводимое представление (представление, семейство операторов к-рого образует вполне неприводимое множество). Вполне Н. п. является (топологически) Н. п. и операторно Н. п.; обратные утверждения, вообще говоря, неверны.