БЕРНШТЕЙНА ТЕОРЕМА

БЕРНШТЕЙНА ТЕОРЕМА

о минимальных поверхностях: если минимальная поверхность задана уравнением . , где f имеет непрерывные частные производные 1-го и 2-го порядков при всех действительных хи y, то F - плоскость.

кривизной. Предложены многочисленные обобщения Б. т., идущие гл. обр. в трех направлениях: 1) Количественные уточнения; напр., получение априорных оценок вида , где - радиус круга, над к-рым определена минимальная поверхность 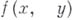, 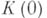- гауссова кривизна поверхности в центре круга. 2) Поиски других априорно задаваемых геометрич. условий, при удовлетворении к-рым минимальная поверхность необходима была бы какой-нибудь конкретной поверхностью: плоскостью, катеноидом и т. д.; напр., если сферич. образ полной минимальной поверхности не содержит нек-рое открытое на сфере множество, то такая минимальная поверхность есть плоскость. 3) Перенесение Б. т. на минимальные поверхности 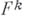размерности , расположенные в евклидовом пространстве ; напр., есл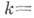и , то при 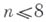всякая минимальная поверхность, однозначно определенная над всем , есть гиперплоскость, а при существуют минимальные поверхности, отличные от плоскости; если же 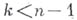, то уже при 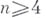можно найти нелинейные минимальные поверхности 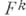, определенные над всем .

Лит.:[1] Берн штейн С. Н., Собр. соч., т. 3, 1960, с. 251-58; [2] Ниче И. С. С., "Математика", 1967, т. 11, № 3, с. 37-100; [3] Оссерман Р., "Успехи. <матем. наук", 1967, т. 22, в. 4, с. 55-136; [4] его же, "Математика", 1971, т. 15, № 2, с. 104-25. И. X. Сабитов.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем сделать НИР

Полезное


Смотреть что такое "БЕРНШТЕЙНА ТЕОРЕМА" в других словарях:

  • Теорема Кантора (значения) — Теорема Кантора: Теорема Кантора о множестве подмножеств в теории множеств Теорема Кантора Бендиксона Теорема Кантора Бернштейна Теорема Кантора Гейне …   Википедия

  • Теорема Кантора — Бернштейна — Теорема Кантора  Бернштейна (в англ. литературе теорема Кантора  Бернштейна  Шрёдера), утверждает, что если существуют инъективные отображения и между множествами A и B, то существует взаимооднозначное отображение …   Википедия

  • Теорема Кантора-Бернштейна-Шредера — …   Википедия

  • Теорема Кантора-Бернштейна-Шрёдера — …   Википедия

  • КАНТОРА ТЕОРЕМА — 1) Множество 2A, состоящее из всех подмножеств множества А, не равномощно ни самому А, ни его подмножеству. Идея доказательства этой теоремы, принадлежащая Г. Кантору (G.Cantor, 1878), получила название канторова диагонального метода и играет… …   Математическая энциклопедия

  • Аппроксимационная теорема Вейерштрасса — В математике аппроксимационной теоремой Вейерштрасса (Стоуна Вейерштрасса) называют теорему, утверждающую, что для любой непрерывной функции на отрезке можно подобрать последовательность многочленов, равномерно сходящихся к этой функции на… …   Википедия

  • БЕРНУЛЛИ ТЕОРЕМА — исторически первая форма больших чисел закона. Б. т. приведена в четвертой части книги Я. Бернулли (J. Bernoulli) Ars conjeсtandi ( Искусство предположений ). Эту часть можно считать первым серьезным трудом по теории вероятностей. Книга издана в… …   Математическая энциклопедия

  • МИНИМАЛЬНАЯ ПОВЕРХНОСТЬ — поверхность, у к рой средняя кривизна Нравна нулю во всех точках. Первые исследования о М. п. восходят к Ж. Лагранжу (J. Lagrange, 1768), к рый рассмотрел следующую вариационную задачу: найти поверхность наименьшей площади, натянутую на данный… …   Математическая энциклопедия

  • Приближение и интерполирование функций —         раздел теории функций, посвященный изучению вопросов приближённого представления функций.          Приближение функций нахождение для данной функции f функции g из некоторого определённого класса (например, среди алгебраических… …   Большая советская энциклопедия

  • Гельфанд, Израиль Моисеевич — В Википедии есть статьи о других людях с такой фамилией, см. Гельфанд. Израиль Моисеевич Гельфанд Дата рождения: 20  …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»