- БЕРНШТЕЙН А НЕРАВЕНСТВО
- 1) Б. н. в теории вероятностей -. уточнение классического Чебышева неравенства, принадлежащее С. Н. Бернштейну (1911, см. [1]); позволяет заменить степенную оценку вероятности больших отклонений на экспоненциально убывающую, см. Больших отклонений вероятности. Именно, если для независимых случайных величин
 с
с
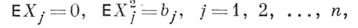
выполняется

(
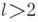 ,
,  - постоянная, не зависящая от
- постоянная, не зависящая от 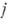 ), то для суммы
), то для суммы 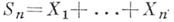 справедливо Б. н.
справедливо Б. н. 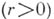 :
:
где
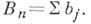 Для одинаково распределенных ограниченных случайных величин
Для одинаково распределенных ограниченных случайных величин  и
и  неравенство (1) приооретает наиболее простои вид:
неравенство (1) приооретает наиболее простои вид:

где
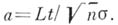 А. Н. Колмогоровым была получена нижняя оценка вероятности в (1). Оценки Бернштейна- Колмогорова используются, в частности, при доказательстве повторного логарифма закона. Нек-рое представление о точности (2) можно получить из сравнения с приближенным значением для левой части (2), даваемым Центральной предельной теоремой в виде
А. Н. Колмогоровым была получена нижняя оценка вероятности в (1). Оценки Бернштейна- Колмогорова используются, в частности, при доказательстве повторного логарифма закона. Нек-рое представление о точности (2) можно получить из сравнения с приближенным значением для левой части (2), даваемым Центральной предельной теоремой в виде

где
 . После 1967 одномерные Б. н. были распространены на многомерный и бесконечномерный случаи.
. После 1967 одномерные Б. н. были распространены на многомерный и бесконечномерный случаи.
Лит.-[1] Бернштейн С. Н., Теория вероятностей, 4 изд., М.-Л., 1946; [2] Колмогоров А. Н., "Math. Ann.", 1929, Bd 101, S. 126-35; [3] Hoeffding W.; "J. Amer. Statist. Assoc.", 1963, v. 58, № 301, p. 13-30; [4] Прохоров Ю. В., "Теория вероят. и ее примен.", 1968, т. 13, в. 2, с. 266-74; [5] Прохоров А. В., "Матем. заметки", 1968, т. 3, в. 6, с. 731-9; [6] Юринский В. В., "Теория вероят. и ее примен.", 1970, т. 15, в. 1, с. 106-7. А. В. Прохоров.
2) В. н. для производной от тригонометрич. полинома или алгебраич. многочлена, дающее оценку этой производной через наибольшее значение самого полинома (многочлена). Если
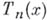 - тригонометрич. полином порядка не выше п,
- тригонометрич. полином порядка не выше п,
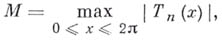
то для любого хвыполняются неравенства (см. [1]):

Оценка неулучшаема; ибо число М= 1 для
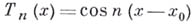 .
.
и

Б. н. для тригонометрич. полиномов является частным случаем следующей теоремы [1]: если
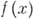 - целая функция степени
- целая функция степени  и
и

то
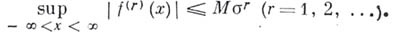
Б. н. для алгебраич. многочленов имеет следующий смысл [1]: если многочлен

удовлетворяет условию

то для его производной
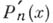 выполняется соотношение
выполняется соотношение
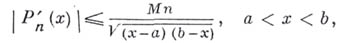
к-рое является неулучшаемым. Как заметил сам С. Н. Бернштейн (см. [1], с. 20), последнее неравенство в сущности вытекает из доказательства Маркова неравенства самим А. А. Марковым.
Б. н. существенно используются при получении обратных теорем теории приближения функций. Имеется ряд обобщений Б. н., в частности для целых функций многих переменных.
Лит.:[1] Бернштейн С. Н., Собр. соч., т. 1, М., 1952, с. 13-42, 269-70; [2] Никольский С. М., Приближение функций многих переменных и теоремы вложения, М., 1969.
Н. П. Корнейчук, В. П. Моторный,
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
